The Topsy Turvy World of Quantum Computing
The weirdest parts of physics are now the cutting edge of computing technology
Strange ideas can come from ordinary places. This one came from Texas. In 1981, John A. Wheeler, the father of the black hole and a theoretical physicist at the University of Texas in Austin, threw a party. The guests were all young physicists with a common interest in the foundations of computing, a topic that Wheeler believed--correctly--would become increasingly important in the years to come.
It was at this party that a conversation with Charles Bennett, an IBM physicist, sparked an idea in the mind of Oxford University researcher David Deutsch. It struck him that computer theory was based on Newton's laws, not the more fundamental description of the universe provided by quantum theory.
At the time, the computer industry was beginning to fret over the future of microchips. How many calculations per second would be ultimately possible, how much heat would this produce, and could silicon survive the constant baking? To help them, computer scientists turned to the theory developed in the 1930s by the pioneer of their field, Alan Turing. But at Wheeler's party, said Deutsch, "I could see immediately that using the laws [of quantum mechanics] would give a different answer."
Deutsch began work on a paper that is now generally regarded as a classic in the field. Published in 1985, it describes how a computer might run using the strange rules of quantum mechanics and why such a computer differs fundamentally from ordinary computers.
Fifteen years later, the revolution that Deutsch started has reached global proportions. Quantum computers are no longer seen as weird curiosities but as the powerful future of the computer industry, and the debate is shifting from whether they will ever become a reality to when they will do so. The excitement is not due to their power, although they undoubtedly will be more powerful than today's models. Their big selling point, the killer app if you like, is that they can solve problems and carry out simulations that are basically impossible on conventional computers.
Such is the potential of these devices that the list of companies funding research programs sounds like a roll call of the world's biggest telecommunications and computer businesses. They include IBM, Hewlett-Packard, Lucent Technologies, AT&T, and Microsoft. There is even a New York Citybased start-up called MagiQ Technologies that hopes to make money by developing intellectual property in this field.
One of the strongest forces driving the development of quantum computers is the fear they will crack with ease secret codes that are impervious to other computers. The alarm bells started ringing in 1994, when Peter Shor of AT&T's Bell Laboratories in New Jersey showed that quantum computers were far faster than their ordinary brethren at factoring numbers.
Finding the factors of large numbers is so difficult for conventional computers that code-makers rely on this weakness of theirs to protect sensitive data. With the development of quantum computers, these codes will be obsolete. As soon as the first modest-sized quantum computer is switched on, governments and their militaries will be forced to concede that many of their codes are unsafe. Understandably, they are keen to find out just what quantum computers can do, and various national laboratories have begun substantial programs, in particular the U.S. National Institute of Standards and Technology in Boulder, Colo.; Los Alamos National Laboratory in New Mexico; and the United Kingdom equivalent, the Defence Evaluation and Research Agency in Malvern.
Aside from its promise for espionage there is the new physics unveiled almost daily by scientists trying to understand quantum information and how to control it. Quantum computers are becoming tiny laboratories in which scientists can test the theories of quantum mechanics with greater precision than ever before. Arguably the strongest team in the world making such discoveries is at the University of Oxford. Smaller groups exist at places such as MIT, Caltech, and a group of Australian universities, with influential individuals scattered throughout the United States, Europe, and Israel. After a late start, Japan has begun a concerted effort to catch up.
Quantum information
Digital information appears mundane stuff. The 0s and 1s of binary code can be easily measured, copied, and moved around. But assign a piece of information to a quantum particle, and it takes on the bizarre characteristics of the quantum world. This fundamental unit of quantum information is called a quantum bit, or qubit (pronounced cue bit), and it is quite different from its classical counterpart.
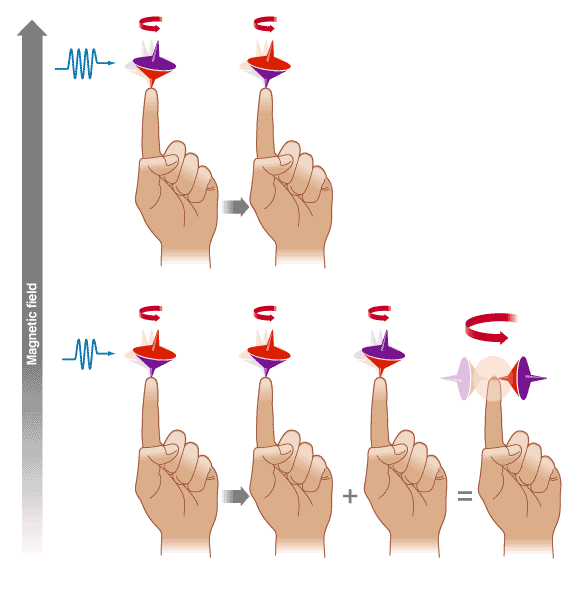
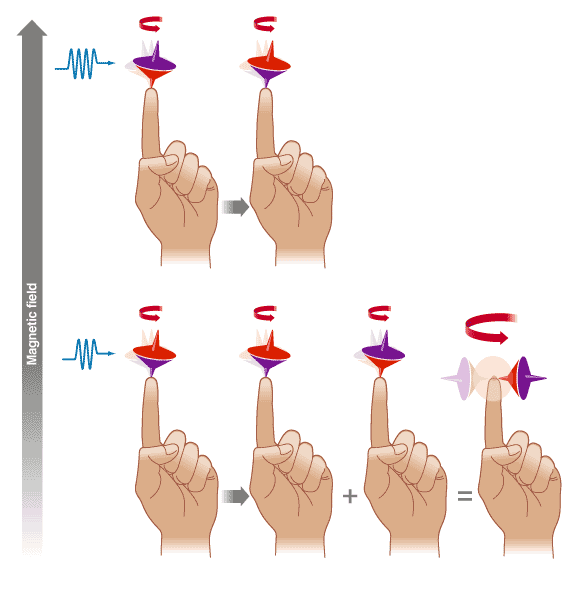
For a start, a qubit can be both a 0 and 1 at the same time. Take the spin of an electron--a property that can be imagined as the spin of a top with its axis pointing either up or down [see figure, above}. The up or down spin can correspond to a 0 or 1. But the electron can also be placed in a ghostly dual existence, known as a superposition of states, in which it is both up and down, a 0 and a 1, at the same time. Carry out a calculation using the electron, and you perform it simultaneously on both the 0 and the 1, two calculations for the price of one.
At first glance, this may not seem impressive, but add more qubits and the numbers become much more persuasive. While 1 qubit can be in a superposition of two states, 0 and 1, two qubits can be in a superposition of four states--00, 01, 10, and 11--representing four numbers at once. The increase is exponential: with m qubits, it is possible to carry out a single calculation on 2m numbers in parallel. With only a few hundred qubits, it is possible to represent simultaneously more numbers than there are atoms in the universe.
Algorithms, entanglement, and error correction
Of course, once the calculation has finished, the answer must be obtained. A simple measurement destroys the superposition, leaving the system in one state or another. Unfortunately, it is rarely possible to determine in advance which state this will be, and that is a problem. The goal is to ensure that the measurement produces the answer of interest, and it can be reached by exploiting the phenomenon of quantum interference. Each of the superposed states has a probability associated with it that has a wavelike behavior--it can interfere with the probabilities of other states destructively or constructively. Getting the desired answer to a calculation means processing the information in such a way that undesired solutions interfere destructively, leaving only the wanted state, or a few more or less wanted states, at the end. The process is known as a quantum algorithm, and its design challenges physicists, mathematicians, and computer scientists. A final measurement then gives the desired answer, or in the case of a few final states, a series of measurements gives their probability distribution from which the desired answer can be calculated.
Quantum algorithms have the potential to be dramatically faster than their conventional counterparts. A good example is an algorithm for searching through lists that was developed by Lov Grover at Lucent Technologies' Bell Laboratories, in Murray Hill, N.J. The problem is to find a person's name in a telephone directory, given his or her phone number. If the directory contains N entries, then on average, you would have to search through N/2 entries before you find it. Grover's quantum algorithm does better. It finds the name after searching through only (check)N entries, on average. So for a directory of 10 000 names, the task would require (check)(10 000) = 100 steps, rather than 5000. The algorithm works by first creating a superposition of all 10 000 entries in which each entry has the same likelihood of appearing in response to a measurement made on the system. Then, to increase the probability of a measurement producing the required entry, the superposition is subjected to a series of quantum operations that recognize the required entry and increase its chances of appearing. (Remember that the recognition is possible because you have the phone number but not the name.)
Coherence/Decoherence: the ability of a quantum system to maintain a superposition of states. Decoherence is the process by which interactions with the environment destroy superposition, forcing a system into one state or another.
Entanglement: the state in which two quantum systems in indeterminate states are linked so that measuring or manipulating one system instantaneously manipulates the second.
Qubit: a unit of information used in quantum computing. It is distinct from an ordinary bit in that it can encode a superposition of values.
Spin: a quantum mechanical property of particles that in certain cases can take only two mutually exclusive values. It is used widely in nuclear magnetic resonance.
Superposition: if a physical system such as a particle can be found in more than one state and its state is unknown, it exists in a superposition of those states. That is, if there are two possible states, the system can be said to exist in both at once until its state is actually measured. Such a measurement collapses the system onto one state or another.
Teleportation: communication between two parties using entangled particles. Through the entanglement the state of one particle can be transferred to another distant particle with which it is entangled.
Vibrational State: the quantized state of the collective motion of ions in a linear ion trap. The vibrational state can encode a qubit and is used to link the ions during calculations.
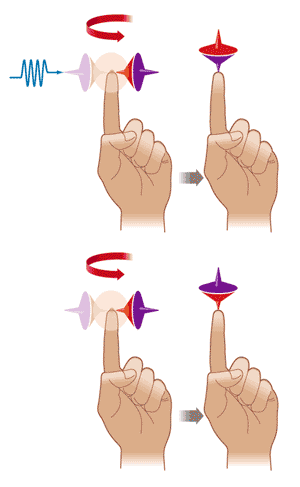
As if superposed values and probability waves were not counterintuitive enough, another strange phenomenon is prominent in the new science of quantum information. In the '30s, scientists fiercely debated whether what quantum mechanics predicted had a real existence or whether its strangeness was due to some deficiency in the theory. In particular, Albert Einstein could not believe that the universe was built as quantum mechanics claimed. So, together with his colleagues Boris Podolsky and Nathan Rosen, he devised a thought experiment to find holes in the new theory.
The thought experiment centers on the behavior of pairs of particles that, according to quantum theory, are joined together--entangled--in a profound way that has no analog in the classical world. Prod one, and it seems the other instantly feels the influence, no matter how far away it might be [see figure, above]. The three scientists pointed out that this process would have to involve a faster-than-light signal passing between the particles--an impossibility. Their conclusion became known as the EPR (Einstein-Podolsky-Rosen) paradox and the entangled particles as EPR pairs.
The debate was resolved by John Bell, a theorist at CERN, the European laboratory for particle physics near Geneva, and the French physicist Alain Aspect. They proved that the Siamese twins of the quantum world, EPR pairs, indeed behave in the way predicted by quantum mechanics. However, the experiment also showed that there is no faster-than-light signal and that entanglement cannot be used for superluminal communication. Rather than communicating, EPR pairs share the same existence, the same destiny, if you like. Entanglement is now one of the key phenomena exploited in quantum information processing. Today the EPR experiment is performed almost daily around the world.
If creating entanglement and superposition has become a commonplace event compared with 10 years ago, quantum information remains fragile stuff. Ordinary interactions with the environment destroy qubits and the information they contain, a process known as decoherence. (Its opposite, coherence, is the ability of a qubit to maintain such quantum characteristics as superposition.) If quantum information is to pass into the world of computer science, a process of error correction is needed to protect against decoherence [see Defining Terms, left].
Initially, physicists believed that such a technique was impossible, because detecting and correcting errors would mean measuring the state of a quantum system and so destroying the information it contained. Still, by the early '90s Deutsch had shown this need not be the case. And in 1994 Andrew Steane at the University of Oxford and Peter Shor at AT&T's Bell Laboratories in New Jersey independently discovered practical quantum error-correction algorithms.
The problem is similar to reproducing in one place a message that has been constructed in another. If the message is sent over a channel or stored in a place noisy enough to distort some of the bits in the sequence, how can the receiver recognize the message? By adding redundancy to the message so that the sender can correct bits that have been distorted.
Shor and Steane came up with the quantum equivalent of sending the same bit three times. The extra qubits are known as ancillas. Measuring these qubits tells the receiver what errors have occurred and how to correct the qubits that are part of the message.
NMR leads the charge
The first big breakthrough for scientists building actual quantum computers came in the mid-'90s, when they discovered how to carry out calculations using the techniques of nuclear magnetic resonance (NMR). The key idea was that a single molecule can act like a tiny computer. Information is stored in the orientation of nuclear spins in the molecule, each nucleus holding one qubit. And the interaction between the nuclear spins, known as spin-spin coupling, serves to mediate logic operations. In a strong magnetic field, these nuclei precess around the direction of the magnetic field at frequencies that depend on their chemical environment.
For instance, in a 9.3-tesla field, a carbon-13 nucleus in a chloroform molecule precesses at about 100 MHz. By zapping the molecule with radio waves tuned to these resonant frequencies, it is possible to manipulate each nucleus individually to carry out logic operations. The manipulation might involve flipping a nucleus from a 1 to a 0, a so-called one-qubit operation or single-bit rotation; or it might involve two linked nuclei in a two-qubit operation, in which the value of one nucleus is flipped in a way that depends on the value of the other.
Chloroform made with the carbon-13 isotope is a good example of a molecule that can act as a two-qubit quantum computer, because its hydrogen and carbon-13 nuclei can be addressed individually by the radio waves. A quantum calculation is then carried out by encoding a program--a sequence of one- and two-qubit operations--as a series of RF pulses. The results are then read out by listening for the magnetic induction signal generated by the precessing nuclei at the end of the calculation. That signal indicates the orientation of the nuclear spin.
Nuclear magnetic resonance sounds like the dream solution to a thorny problem. Nuclei are naturally isolated from the noise of the outside world and so can maintain coherence for many seconds, enough time to perform hundreds of logic operations. In addition, NMR is a mature technology, having been used over many years for imaging and chemical analysis.
But the technique has some severe limitations. Single molecules do not produce a signal strong enough to be observed. Instead, NMR experiments must involve huge numbers of molecules (of the order of 1023) so that their combined magnetic induction signal is large enough to be picked up. (These molecules are usually distributed in a solvent, so the first quantum computers actually have liquid hearts.)
To begin a calculation, the initial state of the computer must be known. But in a material at room temperature, the spin up and spin down states are distributed almost equally and at random. In other words, the state of each of the many computers in solution cannot be known, rendering any subsequent calculation meaningless.
But never say die. In 1997, two groups independently came to quantum computing's rescue. Isaac Chuang, now at IBM's Almaden Laboratory near San Jose, Calif., and Neil Gershenfeld at the Massachusetts Institute of Technology (MIT), in Cambridge, found that they could turn a small natural bias--say, toward spinning up rather than down with respect to the magnetic field--in the nuclei of some molecules to advantage. They could use it to establish a kind of artificial ground state (00 for a two-qubit stystem) from which to start a calculation. At the same time, David Cory, also at MIT, and Amr Fahmy and Timothy Havel, both from Harvard University, in Cambridge, Mass., discovered that by bombarding the sample with radio pulses they could effectively "jam" the signal from all but the ground state.
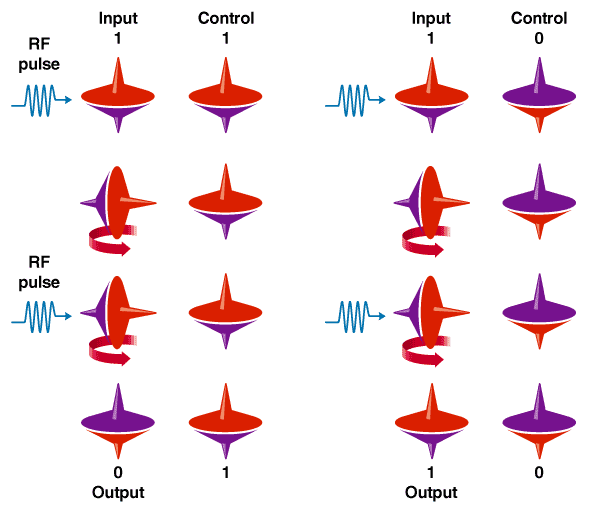
To carry out useful calculations, the computer must be able to perform any logical operation. For quantum computers, there are two logic operations from which all other operations can be derived, rather like the AND and NOT gates in classical computing. One involves rotating a single qubit. The other, carried out on two qubits and called a controlled-NOT gate, flips or fails to flip one qubit depending on the state of another to which it is coupled [see figure, above]. Both these operations are straightforward: simply bombard the liquid sample with the appropriate sequence of radio pulses. Since 1997, these two groups and others, notably at Los Alamos and Oxford University, have built liquid NMR quantum computers with up to seven qubits to perform simple algorithms, one of which even belongs to the mathematical family of Shor's code-cracking formula [see "Quantum Code Cracking Creeps Closer," Spectrum, October 2000].
Unfortunately, quantum computers based on liquid NMR will never be much more powerful than this. The readout signals they produce plummet exponentially with the number of qubits involved in the calculation, because the proportion of molecules found in the appropriate starting state decreases. So scientists do not expect to be able to handle any more than a dozen qubits or so before the signal becomes indistinguishable from the background. Attempts to build machines that can handle more than 10 qubits continue, but if nontrivial quantum computing is ever to become possible, some other approach is needed.
Refrigerated ions
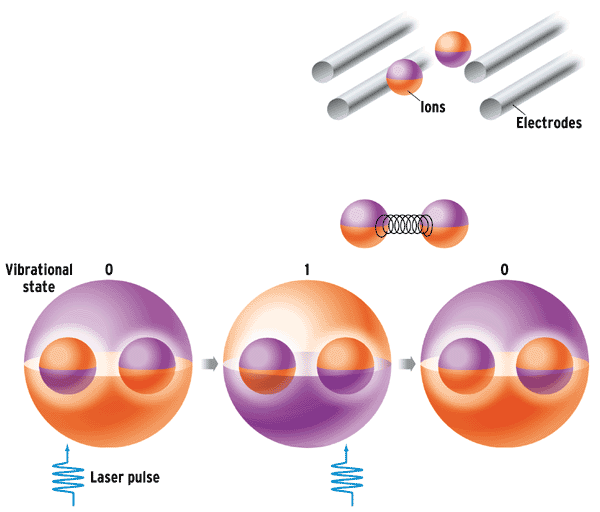
A technology that is less in the public eye than NMR has attracted others. In 1995 Ignacio Cirac and Peter Zoller of the University of Innsbruck, in Austria, suggested using ion traps to build quantum logic gates. The technology behind ion traps is already used for spectroscopy and to improve time and frequency standards, but huge advances are needed for quantum computation. The idea is that a number of ultra-cold ions can be trapped using a device known as a linear radio-frequency Paul trap. This device sets up a high-frequency RF field that holds the ions tightly in two dimensions but only weakly in the third dimension. Because the ions have the same charge, they repel each other and tend to arrange themselves in a straight line, equally spaced, like beads on an elastic string. The arrangement allows them to vibrate as a group in ways important for quantum computing.
The qubits are initially stored in the internal spin states of the ions relative to a background magnetic field. They are written to the ions using a pulsed, oscillating magnetic field, which flips the bits or places them in a superposition of up and down states, depending on its duration. An advantage of ion traps is that this superposition is extremely robust, lasting for at least as long as the qubits in NMR, ample time to carry out the desired logic operations.
Basically, a pulse of energy equal to the difference between the quantum state of the ion and the vibrational state of the two ions (0 or 1) leads the ion to swap its internal state for the vibrational state. A similar pulse to the other ion performs another swap, transferring the original state of the first qubit to the second.
To share the qubits between the ions, scientists turn to the ion vibrations. The aim is to chill the ions until as a group they are absolutely still. This is the ground state of the system. Inject a little energy, and the ions begin to vibrate. But being quantum particles, the ions can exist in a superposition of the ground state and the vibratory state, so the vibration can be used to store a qubit. Because the ions all take part in the vibration, this qubit is shared among them. It's as if this collective motion is a kind of databus, allowing all the ions to temporarily share the information and become entangled. This sharing allows the IF and THEN type operations that are the building blocks of computer logic gates. For example, an instruction might be: IF the vibrational state is 1, THEN flip the qubit in the first ion's internal spin state. Researchers at the National Institute of Science and Technology (NIST) have already demonstrated that a string of four ions can be entangled and have said that more should be possible.
At least five groups around the world are working on ion trap quantum computers, but David Wineland's team at NIST is widely regarded as the leader. His group has built a 2-qubit logic gate using a single beryllium ion cooled to its vibrating ground state. Using a laser focused on the ion, the group superimposes on the background magnetic field a second magnetic field with a magnitude that varies with the position of the ions. The ion's vibration causes it to experience an oscillating magnetic field, and when the frequency of the oscillation matches the energy difference between the ion's two spin states, energy is transferred from the spin to the vibrational state, mapping the quantum information to the vibrational from the spin state [see figure, above]. This is the basis of a controlled-NOT gate and was realized in 1995 only a few months after Cirac and Zoller's announcement. Reading the data involves scattering light off the ion, since a spin up ion can be made to scatter strongly, while a spin down ion will scatter hardly at all.
Ion traps, too, have their limitations. One is the short decoherence time of the qubits after transfer to the vibrational "databus." Because the ions are charged, the vibrations are strongly influenced by stray electric fields, causing decoherence. Nonetheless, the group is confident that this tendency can be overcome by isolating the trap better from the environment. Ion traps also suffer from problems of scalability. The more ions there are in the trap, the greater the risk of tapping into uncontrollable vibrational states and so destroying the calculation. The next step will be to build adjacent traps, each holding only a few ions, and sending quantum information from one trap to another, either by physically moving the ions or by a phenomenon peculiar to quantum information called teleportation.
The alternatives
While liquid NMR is doomed because of the problems of working at room temperature, several groups are looking into carrying out NMR-type manipulations on single atoms in the solid state. A proposal from Bruce Kane at the University of Maryland in particular has attracted attention. His idea is to bury an array of phosphorus atoms in silicon and overlay it with an insulating layer, on top of which sits a like array of electrodes, each of which can apply a voltage to the atom beneath it. The ingenious aspect of this setup is how Kane proposes to control the spin of each nucleus.
Just as in NMR, the spin of the nuclei can be flipped by being zapped with radio waves of just the right energy--but, of course, these radio waves would flip every nucleus. Now phosphorus atoms have a single electron in their outer shell that interacts with the nuclear spin in a complex way. Applying a voltage to the atom changes the energy required to address both the nuclear and the electronic spin, and therefore it changes the frequency of the radio waves needed to flip the nucleus. So by applying a voltage to a specific electrode and zapping the array with the new frequency, it is possible to address a single nucleus.
But to perform a controlled-NOT logic operation, two qubits have to become entangled. Kane also has a way of doing this. Voltages applied between adjacent phosphorus atoms in the array can turn on and off the interactions between the outer electrons in each atom, allowing two-qubit operations.
Of course, the theory is all very well. The difficulty is actually building such a device, and Kane's collaborators are already working on it. At the Centre for Quantum Computer Technology at the University of New South Wales, in Australia, Robert Clark heads a team that is hoping to overcome many of the obstacles Kane's device faces. First up is the difficulty of creating the atomic array and preventing the phosphorus atoms from migrating within the silicon.
Kane is setting up a lab to study another challenging aspect of his device: the readout. Once the one- or two-qubit operation has been completed, the result has to be read out from the nuclear spins. Once again, Kane relies on the link between nuclear and electronic spins to get an answer. By very carefully measuring the spin of the electron, he said, it is possible to infer the spin of the nucleus. Measuring the spin of a single electron has never been done, but Kane said this should be possible shortly.
Kane's idea has attracted so much attention because many of these logic gates can be linked together to form a large quantum computer, though doing so may take some time. New South Wales's Clark believes that a handful of qubits might be possible in the medium term.
The quantum phenomena of superconductivity may also prove useful for building quantum computers. In 1999, at the Delft University of Technology in the Netherlands, a team designed a superconducting circuit in which superposed counter-rotating currents could prove useful for storing and manipulating qubits. The circuit consists of a loop with three or four Josephson junctions for measuring the circuit's state. The fact that it is made by conventional electron-beam lithographic techniques makes it particularly conducive to large-scale integration. However, superconducting circuits have short decoherence times, and today's techniques for measuring the states of the circuits are too invasive for useful manipulation of qubits.
A more advanced solid-state technology is the quantum dot, essentially a semiconductor trap holding a discrete number of electrons. These have been studied since the early 1990s because the trapped electrons act like artificial atoms, with their own periodic table and chemistry. Then in 1998, David DiVincenzo of IBM and Daniel Loss of the University of Basel, in Switzerland, proposed using quantum dots as the building block of a quantum computer, and a variety of ideas have since been put forward for exploiting the dots' quantum properties for computation. One idea is a two-qubit system consisting of two electrons shared by four quantum dots in a square. The electrons, seeking to minimize their energy, occupy opposite corners of the square, and since this arrangement has two configurations, they exist as a superposition that is manipulable through electrodes at the corners of the square. A number of other techniques involve reading and writing data to the dots with laser pulses and placing a single nucleus at the center of each dot that can be addressed with NMR techniques, rather as in Kane's proposal.
The problems in scaling up many of these ideas have persuaded many scientists that if quantum computing is to become useful any time soon, it will have to involve networking small quantum computers together. But sending quantum information from one place to another is tricky. One option is to physically move the qubits, but then they would be liable to decoherence. In 1993, however, Charles Bennett, from IBM's Thomas J. Watson Laboratory in Yorktown Heights, N.Y., and a few colleagues came up with a different option: teleportation.
Teleportation utilizes the deep link that entanglement sets up between one point in the universe and another. Bennett theorized that entanglement could act as a kind of phone line down which to send quantum information--in other words, create an entangled pair of particles and send one of them to the receiver while keeping the other [see "Quantum Teleportation"]. This process links these two points in a way that allows the exchange of quantum information from one qubit to another.
The first modest-sized quantum computer may make many encrypted data files insecure
Bennett and his colleagues had to wait four years to see their predictions verified. In 1997, in a small room at the University of Innsbruck, in Austria, a group of physicists led by Anton Zeilinger performed the first teleportation experiment. Zeilinger's travelers were photons and he was sending them only a meter or so, from one side of the lab to the other. Today, more than three years later, Zeilinger is working on the next step, which is to teleport photons over distances of a kilometer.
Soon after Zeilinger's breakthrough, Cirac and Zoller proposed that teleportation could become the basis of a kind of quantum Internet. And in March of 2000, Seth Lloyd and Selim Shahriar at MIT and Philip Hemmer at the U.S. Air Force Research Laboratory, in Lincoln, Mass., suggested sending entangled photons over optical fibers to nodes containing cold atoms that would absorb the photons and so store the entanglement. This entanglement could then be used for error correction, teleportation, and various other valuable applications. A number of groups are working on this idea, including Jeff Kimble at the California Institute of Technology and Eli Yablonovitch at the University of California at Los Angeles. They hope to have a three-node network running within 10 years.
Some scientists hope for even greater things from entanglement, believing it will be so useful that it will one day be traded as a currency over the quantum Internet. Considerable progress will be required before anything remotely like that becomes possible. Even so, the pace of innovation in quantum computing has already exceeded most scientists' wildest dreams. Only five years ago, many were confident that quantum computers would not be built for 20 years, yet NMR proved them wrong within a year. Only the bravest forecaster would dare to predict how the field will stand five years from now.
With only a few hundred qubits it is possible to represent simultaneously more numbers than there are atoms in the universe
Numbers to Ponder
With only a few hundred qubits it is possible to represent simultaneously more numbers than there are atoms in the universe
Spectrum Editor: Samuel K. Moore
About the Author
JUSTIN MULLINS [p. 42], a contributing editor, is a freelance science writer based in Oxford, England. He is a consulting technology editor for New Scientist.
To Probe Further
For an overview of quantum computing techniques and the peculiarities of quantum information, try Introduction to Quantum Computing and Information, edited by Hoi-Kwong Lo, Sandu Popescu, and Tim Spiller, and published in 1998 by World Scientific (Singapore).
Some important papers in quantum computing include: "Bulk Spin-Resonance Quantum Computation," by N. Gershenfeld and I. L. Chuang, Science, Vol. 275, p. 350 (1997); "Quantum Logic Gates in Optical Lattices," by G. Brennen, C. Caves, I. Deutsch, and P. Jessen, Physics Review Letters, Vol. 82, p. 1060 (1999); "A Silicon-Based Nuclear Spin Quantum Computer," by B. E. Kane, Nature, Vol. 393, p. 133 (1998); and Teleportation and the Quantum Internet, by S. Lloyd, M. Shahriar, and P. Hemmer, available from the Los Alamos Archive (https://xxx.lanl.gov).
An informative Web site explaining quantum teleportation is https://info.uibk.ac.at/c/c7/c704/qo/ photon/_teleport/index.html.
Nuclear magnetic resonance (NMR) is explained in an on-line book at https://www.cis.rit.edu/htbooks/nmr/. The author is Joseph P. Hornak.