The Hunt for the Magnetic Monopole
If magnets don’t have to have two poles, it could lead to an entirely new class of devices

One of the very first facts you learn about electromagnetism—long before you walk into your first physics class—is that every magnet has two poles. Cut a bar magnet in half and you wind up with two magnets, each of which has its own north and south poles. And that’s true for every single object in our experience that boasts a magnetic field—whether it’s the entire Earth or an iron atom. There are no solitary poles.
Strangely, though, there is no fundamental reason why that has to be the case. In fact, there are a few good reasons to suspect that there might be single-poled magnetic objects—magnetic monopoles—floating about in the universe. If these particles exist, they are probably quite rare, but that hasn’t stopped physicists from looking for them. Here’s why: If they exist, they could help answer long-standing questions about the nature of the universe, shedding light on the way fundamental forces of nature are tied together.
So over the past few decades, physicists have scoured Antarctic ice and lunar dust and scrutinized rocks culled from ocean beds and polar volcanoes. They’ve tried to create monopoles in particle colliders and have searched for signatures in cosmic rays that collide with Earth.
In every case so far, the search has come up dry. But a few years ago, my colleagues and I, along with other research groups, came across evidence of something that looks and acts very much like a naturally occurring monopole would. Our monopoles are confined to particular materials, and they arise only when the spins of atoms are aligned in just the right way. But unlike their still elusive, relatively unconstrained brethren, they do offer some hope of new technologies. One day, we might be able to manipulate magnetic charges much as we control the flow of electric charges today. It’s almost impossible to predict where this new capability could lead; we could see devices that are capable of performing computations or storing information or energy in entirely new ways. But before we can know what monopoles can do, we must get to the bottom of how they behave.
Most of what we know about magnetic fields dates back to the mid-19th century, when James Clerk Maxwell debuted a set of equations that demonstrated that electric and magnetic forces both stem from a single force: electromagnetism. Maxwell showed there is symmetry in this unification: Changing magnetic fields create electric currents, and moving electric charges create magnetic fields. But this symmetry has its limits. Electric charges can be positive or negative, but magnets are dipolar. They always contain two “magnetic charges”: a north and a south pole.
This asymmetry was more or less just a curiosity until 1931. That’s when physicist Paul Dirac showed that the existence of a magnetic version of charge—a magnetic monopole—could help explain a seemingly arbitrary fact: why electrons and other charged particles have only quantized amounts—that is to say, integer multiples—of a fundamental electric charge. That realization offered the possibility that, even if they are far removed from our everyday experience, magnetic monopoles just might exist. More recent theoretical work has revitalized this idea, because the particles also pop up in grand unified theories that attempt to tie fundamental forces of nature together.
These monopoles would be free-floating particles, at liberty to flit about the vacuum of space. But in 2008, three theoretical physicists—Claudio Castelnovo, Roderich Moessner, and Shivaji Sondhi—argued that we should be able to find something like them inside special crystals on Earth. Such monopoles wouldn’t be fundamental particles; they would exist only in the material and would form from the collective behavior of other particles. But they would technically be single magnetic charges, and they would interact with one another in much the same way that fundamental monopoles probably would.
The team proposed looking for these trapped monopoles at temperatures close to absolute zero in spin ice, a peculiar class of materials with ions arranged in four-sided pyramids called tetrahedra. These tetrahedra are stacked together to make a crystal called a pyrochlore.
The atoms at each corner of the pyramids in a pyrochlore are magnetic dipoles. Just like a bar magnet, they have a magnetic field that emerges from one side (what physicists tend to call “north” by convention) and curves around the atom so that it eventually enters the opposite end (“south”). As shorthand, physicists represent this magnetic field as a north-pointing arrow centered on the atom. This arrow is an indicator of magnetism, and it also corresponds to the atom’s “spin”—its intrinsic angular momentum. Spin is a quantum mechanical concept: Atoms may not physically spin, but their angular momentum is reflected in other ways, such as the trajectories that daughter particles take when radioactive atoms decay.
Just like bar magnets, these spins interact with one another electromagnetically and try to align themselves so that they are parallel or antiparallel to one another. But what makes spin ices special—and what gives them their name—are the configurations these spins are forced into by the geometry of the crystal.
When the temperature of the crystalline material is relatively high, the forces that try to align the spins are easily overwhelmed by thermal fluctuations. The spins are oriented at random and can easily change direction. When the material is cooled to just a few degrees above absolute zero, the forces between spins begin to dominate. The spins of the atoms naturally begin to align into the lowest, most stable energy state: a configuration in which two of each tetrahedron’s four spins point toward the center of the pyramid and two point outward.
This “two-in, two-out” configuration is called the ice rule, so called because it’s analogous to the way that hydrogen bonds form in ordinary water-ice crystals. For each oxygen atom, two hydrogen ions sit close in and two sit farther away. Spin ices tend to obey the ice rule, but the alignment process isn’t perfect. Sometimes defects form as the sample cools. In other cases, a bit of thermal energy can cause a spin to flip its orientation. In the end, some tetrahedra wind up with three spins pointing in or out and just one in the opposite direction. Researchers have known about these rule violations for a while, but Castelnovo and his colleagues argued that they might have a much bigger physical significance.
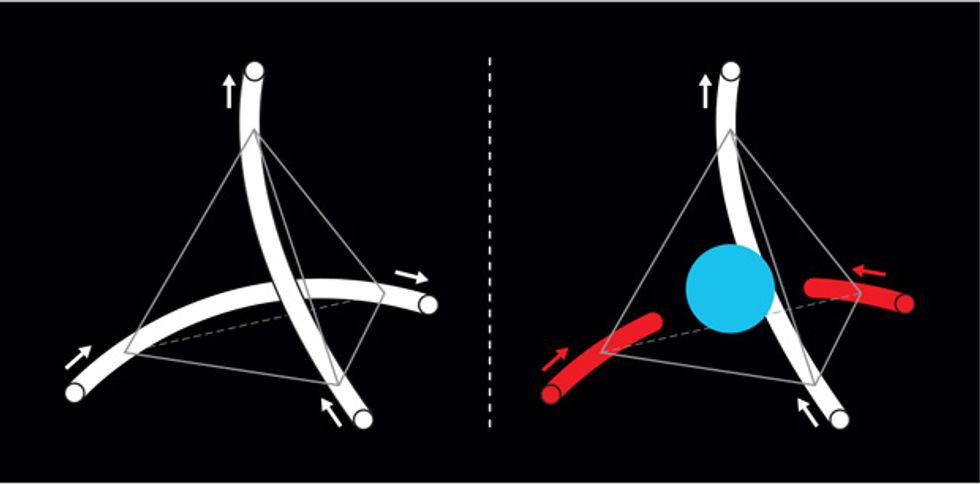
Because magnetic fields extend well beyond each atom, the researchers suggested that we think of the spin on each atom as an extended dumbbell. The connecting bar is centered on the atom’s nucleus and ends in two distinct magnetic charges: a north pole at the center of one tetrahedron and a south pole at the center of another. When you look at the center of one of those tetrahedra, the poles from the four corners will either cancel each other out or add together.
In the case where ice rules are obeyed, the two north poles and two south poles cancel each other out. But here’s where it gets interesting: When the ice rules are not obeyed—if, for example, there are three spins pointing inward and one pointing outward—then the three north poles and one south pole in the center will give rise to a single, north magnetic pole. Voilà! There’s your monopole. Similarly, a one-in, three-out configuration would make a single, south magnetic monopole.
And that’s not all. Because each vertex of a tetrahedron is also shared with a neighbor, the spin that violates the ice rule in one tetrahedron would also do so in another, creating a second monopole one tetrahedron away with the opposite polarity. So, for every monopole, there will be an oppositely charged monopole. If that same spin flips, or rotates 180 degrees, the spin-ice rules will be fulfilled and the pair will essentially be annihilated.
To be considered true magnetic particles and not just magnetic anomalies, these spin-ice monopoles should be able to move. And indeed, Castelnovo and his colleagues noted that two monopoles should be able to separate from one another and move independently through the spin ice. Flip another spin in a monopole’s tetrahedron and the spins will once again balance out there but become unbalanced in a neighbor. The monopole will have effectively jumped from one tetrahedron to another. That raised the tantalizing possibility of creating the magnetic analogue of electric current: “magnetric current.”
Once this proposal appeared in Nature in January of 2008, it didn’t take long for experimentalists around the world to go on the hunt. At the time, I was working as a postdoc at the Helmholtz Center Berlin for Materials and Energy. My collaborators and colleagues—Alan Tennant and Santiago Grigera—had already been working on spin ices for several months. They had been examining some anomalous behavior that set in when a particular spin ice—a compound made of oxygen, titanium, and the rare earth element dysprosium—was cooled to below 0.6 kelvin. When the theory paper came out, they changed focus, and I joined my colleagues—Tennant, Grigera, and a third team member, Kirrily Rule—to hunt for evidence of magnetic monopoles.
We used a powerful probe we already had on hand: neutron beams. Because they have no electric charge, neutrons pass easily through most of the space in a material, scattering only when they collide with the tiny nuclei at the center of atoms. But they also have intrinsic magnetic moments, so they can be deflected by the magnetic fields of atoms. Shine a beam of neutrons through a material and the pattern they make on the other side can tell you certain things about the magnetic structure that caused the neutrons to diffract. It’s the standard way physicists study subjects as wide-ranging as the structure of proteins, strains in jet engine blades, and the magnetic interactions in superconductors.
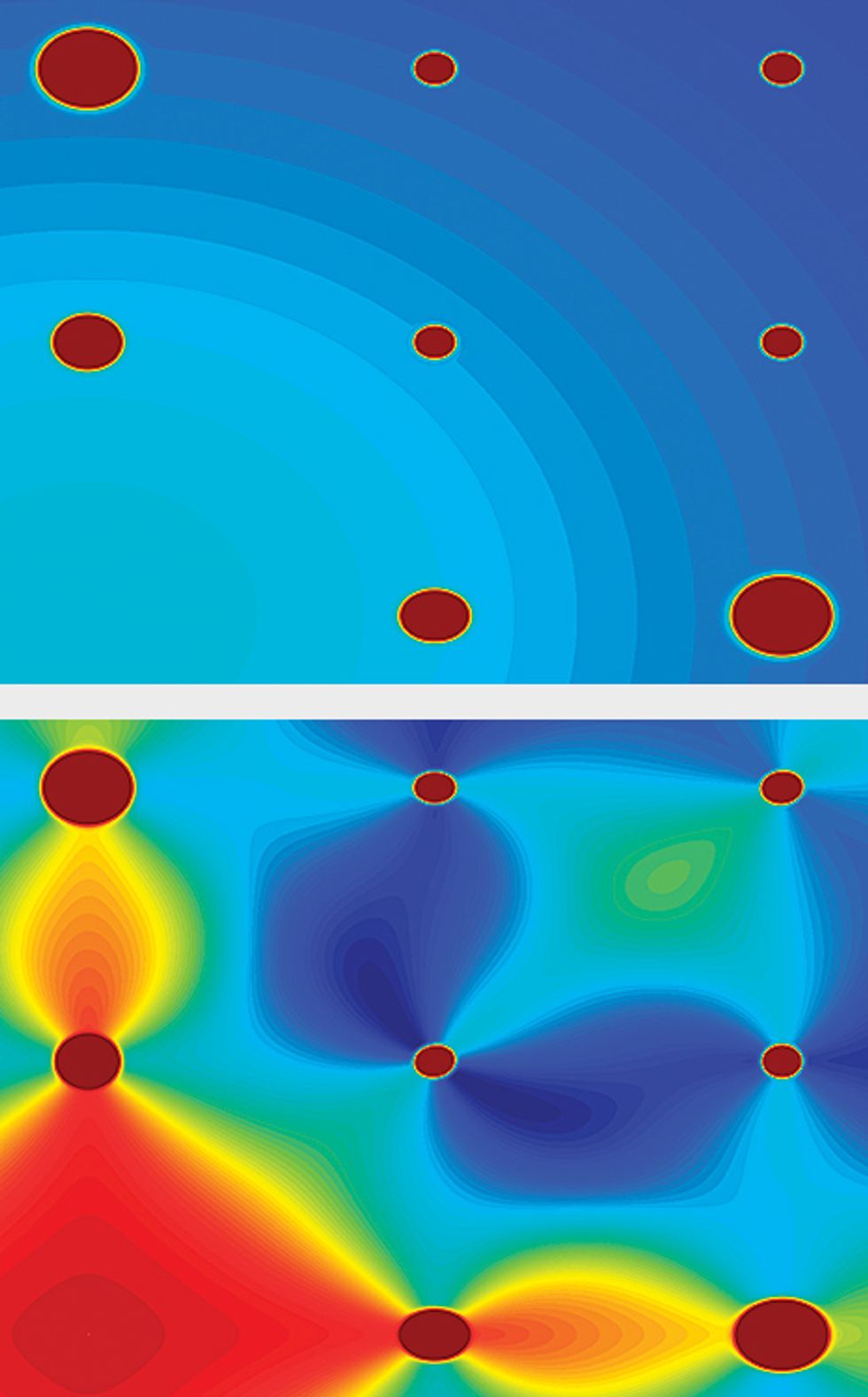
Bending Neutrons
Images: D.J.P. Morris
Physicists can look for polarization tubes, or strings, that link monopoles by shining neutrons through a spin-ice sample. These idealizations show what the resulting neutron-scattering data might look like if a sufficiently strong magnetic field is used to align all the spins so that no strings exist [top] and if this magnetic field is turned off so strings can form [bottom].
In a spin ice, neutrons are particularly well suited to picking up on correlations between spins—how closely related the alignment of one spin is to another. We think of these alignments as “polarization tubes”—chains of spins that by convention flow from south to north. In an ordinary tetrahedron that obeys the ice rules, you’ll have two such tubes flowing through the center; each one enters the tetrahedron by a spin with its north side pointing in and exits by one with its north side pointing out. When the ice rules are broken, just one polarization tube will flow all the way through the tetrahedron and two other polarization tubes will terminate at the center. Those endpoints are where we should expect to see monopoles. Otherwise we might simply see a material containing polarization tubes without endpoints—essentially just loops.
When neutrons scatter off polarization tubes, they leave distinctive patterns in the locations of neutrons that hit our detectors. But inferring the structure responsible for this pattern is difficult to do. If you could visualize all the polarization tubes in a spin ice, you’d have what would look like a bowl of spaghetti. If you tried to follow a single strand through a pile, you’d quickly become lost in a 3-D knot.
To simplify matters, our group devised a way to, in effect, pull on that tangle of spaghetti with a fork, separating out the polarization tubes by applying a magnetic field. When a strong enough magnetic field is applied to a spin ice, all of the spins orient themselves along the field, and because they are all pointing in the same direction, the polarization tubes are erased. As the magnetic field is lowered back down, spins begin flipping against the magnetic field as the strength of their interactions starts to overcome the external magnetic field. These flipped spins form short “strings”—sections of polarization tube that are easier to see in the neutron data. When we looked at the data as a function of the applied magnetic field, we found that the strings grow along the field, but they also meander a bit.
This is consistent with what we would expect to see if monopoles were present and had enough energy to migrate away from one another, leaving behind a string of flipped spins. But we needed a way to confirm there were in fact monopoles at the end of the strings.
Fortunately, some colleagues of ours in Berlin—Clemens Czternasty, Bastian Klemke, and Michael Meissner—were working on just such an experiment. They were investigating the spin ice’s heat capacity, a measure of how much energy is needed to change a material’s temperature. Heat capacity is linked to the number of different configurations a material can take on. For water, it corresponds to the number of possible arrangements of hydrogen and oxygen atoms. For a spin ice, it’s related to the number of spin orientations. The number of possible configurations is linked to how much energy is available to the materials, so heat capacity is a very sensitive measure of the state of the system.
The Berlin team found that very little heat was needed to raise the temperature at very low sample temperatures. The drop-off in heat capacity as the temperature goes down was so sharp that the team initially thought something was wrong with the equipment. But repeated measurements confirmed the result. When we presented the data to Castelnovo and his colleagues, they first attempted to make sense of it with a simple model of the material that was based on spins alone. But they found that the only way they could get a good fit to the data was to posit the existence of monopoles that have their own physical interactions. It was estimated that we created about 600 monopoles per cubic centimeter.
Armed with this evidence, our team started preparing a research paper. But we soon found out that other teams were also on the case. In March 2009, a pair of theoretical physicists based in France reported in Nature Physics that they could fit some old magnetic data better if the existence of magnetic monopoles was assumed. This made a bit of a media splash, but we realized that we had an even more detailed story to tell, so we remained undeterred. Then, in May 2009, I saw a presentation on a hunt by Hiroaki Kadowaki’s group at the Tokyo Metropolitan University, at the International Conference on Neutron Scattering. By the time we submitted our paper to Science in July, we found out that two other papers were also under consideration by the magazine.
In the end, three experimental teams all reported evidence of magnetic monopoles in quick succession. Our Science paper appeared in September alongside one from a British-French group led by Tom Fennell, then at the Institut Laue-Langevin. That team reported evidence that strings lengthen in spin ice as the temperature drops, which suggested that if monopoles were present, they were migrating away from one another in the sample. Around the same time, Kadowaki’s team reported neutron scattering results that seemed to match simulations of scattering as a function of monopole density.
One of the questions I was asked a lot after our Science paper came out was whether the monopoles we’d found in spin ice could be considered “real” magnetic monopoles.
They’re certainly not the ones that particle physicists have been dreaming about for decades. The magnetic monopoles in spin ice can’t exist in free space. In a sense, they’re not real particles at all. Physicists prefer to call them quasiparticles: particle-like entities that are artifacts of the collective behavior of other particles. Quasiparticles are common. Many modern semiconductor devices, for example, rely on the flow of holes—positively charged “particles” that are really just the absence of electrons.
If these monopoles are not the objects searched for by particle physicists, can we justifiably call them magnetic monopoles? The heat capacity measurements our team performed suggest that spin-ice monopoles really do seem to carry a magnetic charge, and their interactions mimic the basic way that positive and negative magnetic charges would interact in vacuum.
At the same time, they’re trapped particles. And that’s raised a number of interesting problems. In 2011, one of my Berlin colleagues, Klemke, realized that all the published heat capacity data below 0.6 K were different. What’s more, the magnetization measurements in that temperature range don’t agree with theory. Some theorists have suggested that these inconsistencies exist because, at low temperatures, there is little energy available to flip spins. As it equilibrates, a spin ice could get trapped in an especially unfavorable configuration that is difficult to escape from without some very well-coordinated, simultaneous spin flipping. That means it will take a long time for the material to find the most energetically favorable configuration. In fact, in April, a Canadian group led by David Pomaranski reported that at very low temperatures, spin ice can take weeks to relax; at just one degree above absolute zero, it might take a hundredth of a second.
Because we’re still sorting out the basic physics, we’ve only just begun to start thinking about applications. One intriguing possibility is “magnetricity”—a magnetic form of electricity. With the right magnetic field, it might be possible to draw monopoles through spin ice in much the same way that voltage is used to draw current through wires. The peculiarities of the spin-ice geometry won’t make magnetic current nearly as simple, however. Because moving monopoles leave a trail of flipped spins behind them, it’s impossible to drive a second monopole along the very same path. That rules out a monopole direct current, but it does leave the window open for monopole alternating current and devices.
Because the spins can flip in a spin ice, the material might also be able to screen a magnetic field and store magnetic energy much as a dielectric does. What’s more, there is some evidence to suggest that it might be possible to dope the material, similarly to the way that impurities are added to a semiconductor to boost its charge-carrying properties. Last year, experiments showed that monopoles could be made to move more slowly through a spin ice if more magnetic ions were added to the mix. If the spin ice can be doped to alter the speed of monopoles through the material, it’s not unreasonable to imagine magnetic analogues to basic electrical device components like capacitors and junctions.
But there are a few big stumbling blocks we’d have to overcome before we could get anywhere close to making practical magnetronic devices. One is the purity of the samples: Even tiny structural defects can block the flow of monopoles. The other is temperature. To freeze a spin ice and create monopoles, you must cool such materials to very low temperatures, typically on the order of one degree above absolute zero—about 1 K, or –272 °C. It’s unclear whether we can create a material that can undergo a spin-ice transition at more practical temperatures. The magnetic moments of its atoms, or the interactions between them, would have to be enormous to counteract the scrambling effects of thermal energy at higher temperatures, and no such material is currently known to exist.
One alternative monopole system that has emerged is “artificial spin ice.” These man-made materials are two-dimensional systems that can be made from nanoscale patches—either islands or wires—of a ferromagnetic material such as cobalt. A patch’s dimensions are chosen so the magnetic moments of the atoms inside it point toward a vertex between neighbors. If these patches are arranged in either a honeycomb or a square structure, you can get their magnetic moments to obey ice rules. A square lattice will obey the same two-in, two-out rules as ordinary spin ice. In a honeycomb lattice, where three patches meet at each vertex, there is always an excess magnetic charge.
How do we know that these charges exist? Incredibly, they can be imaged using magnetic force microscopy. In 2010, an Imperial College London team observed artificial magnetic monopoles and was even able to watch them move under influence of a magnetic field. These materials have the benefit of being stable at room temperature, and some researchers have proposed that they might make useful memory devices. But artificial spin-ice patches currently have dimensions in the 100-nanometer range, making them gigantic by existing industry standards.
Still, it’s early days for the magnetic monopole, and I wouldn’t rule out powerful applications that have yet to be imagined. A magnetronic revolution might be just over the horizon.
About the Author
In 2009, Jonathan Morris was among those who found single magnetic charges—magnetic monopoles—inside crystals called spin ices. Soon to join the faculty at Xavier University, in Cincinnati, Morris was at the time a postdoc at the Helmholtz Centre Berlin for Materials and Energy. The flurry of media attention that ensued included a mention on the U.S. sitcom “The Big Bang Theory.” “It was kind of surreal,” he says.