MIT and IBM Find Clever AI Ways Around Brute-Force Math

Since the days of Isaac Newton, the fundamental laws of nature all ultimately reduce to a vital, broad set of equations. Now researchers have found a new way to use brain-inspired neural networks to solve these equations significantly more efficiently than before for numerous potential applications in science and engineering.

In modern science and engineering, partial differential equations help model complex physical systems involving multiple rates of change, such as ones changing across both space and time. They can help model all sorts of things, such as the flow of air past the wings of an airplane, the spreading of a pollutant in the air, or the collapse of a star into a black hole.

To solve these difficult equations, scientists traditionally used high-precision numerical methods. However, these can be very time-consuming and computationally resource-intensive to run.

Currently, simpler alternatives exist, known as data-driven surrogate models. These models, which include neural networks, are trained on data from numerical solvers to predict what answers they might produce. However, these still require a large amount of data from numerical solvers for training. The amount of data needed increases exponentially as these models grow in size, making this strategy difficult to scale, says study lead author Raphaël Pestourie, a computational scientist at the Georgia Institute of Technology in Atlanta.

In a new study, researchers developed an approach to developing surrogate models. This strategy uses physics simulators to help train neural networks to match the output of the high-precision numerical systems. The aim is to generate accurate results with the help of expert knowledge in a field—in this case, physics—instead of merely throwing a lot of computational resources at these problems to find solutions using brute force.

Researchers have found that numerical surrogates (symbolized here as a cartoon of James Clerk Maxwell) can arrive at solutions to hard mathematical problems that had previously required high-precision, brute-force math—symbolized by the Maxwell daguerreotype. MIT

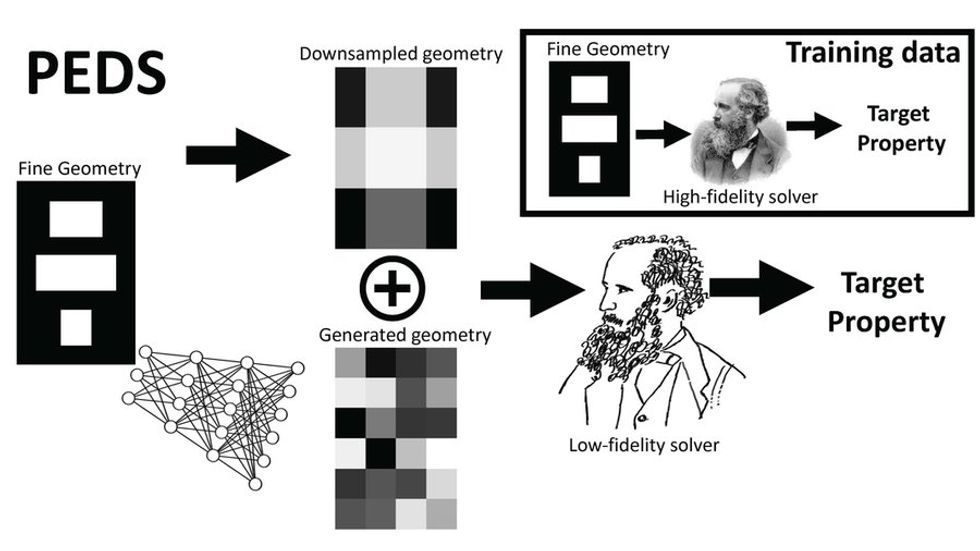
The scientists tested what they called physics-enhanced deep surrogate (PEDS) models on three kinds of physical systems. These included diffusion, such as a dye spreading in a liquid over time; reaction-diffusion, such as diffusion that might take place following a chemical reaction; and electromagnetic scattering.

The researchers found these new models can be up to three times as accurate as other neural networks at tackling partial differential equations. At the same time, these models needed only about 1,000 training points. This reduces the training data required by at least a factor of 100 to achieve a target error of 5 percent.

“The idea is quite intuitive—let the neural networks do the learning and the scientific model do the science,” Pestourie says. “PEDS shows that combining both is far greater than the sum of its parts.”

Potential applications for PEDS models include accelerating simulations “of complex systems that show up everywhere in engineering—weather forecasts, carbon capture, and nuclear reactors, to name a few,” Pestourie says.

The scientists detailed their findings in the journal Nature Machine Intelligence.

Updated 5 Feb 2024 to remove incorrectly stated laws of nature. Spectrum regrets the error.