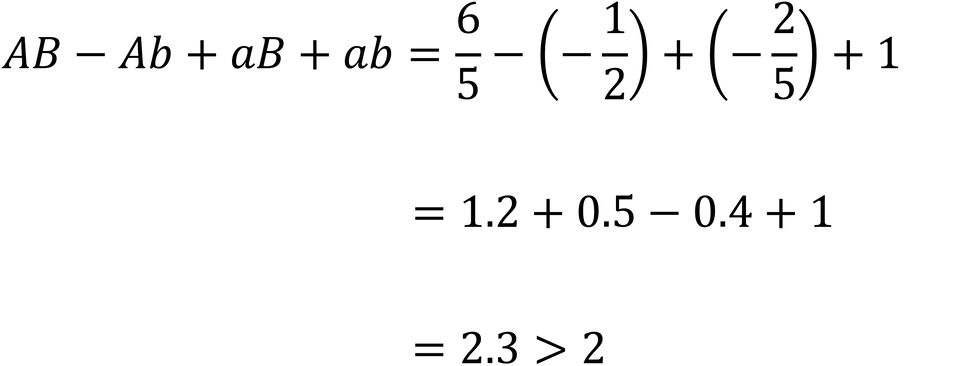When pushed to explain why quantum computers can outspeed classical computers, stories about quantum computing often invoke a mysterious property called “entanglement.” Qubits, the reader is assured, can somehow be quantum mechanically entangled such that they depend on one another. If more detail is needed, the reader is told that entanglement links qubits no matter how far apart they are—so long as the qubits are “coherent.”
For the reader, things are far from coherent. Sure, entanglement is an important aspect of quantum computing. But what exactly is it?
In a few words, entanglement is when multiple objects—such as a pair of electrons or photons—share a single quantum state. Like threads in a tangle of yarn, entangled objects cannot be described as independent entities.
That explanation might be poetic, but it shouldn’t be satisfying. Things are not so simple or concrete. But with a little bit of high-school-level math (near the end of this story), our intuitions—based on a lifetime of classical physics—can be retrained and redirected just a bit.
However, we should also make the following disclaimer: No brief explanation can be expected to convey a comprehensive understanding of quantum mechanics. Our goal is simply to illustrate the basic concepts behind entanglement, so the reader can gain a more thorough understanding of what’s actually going on in this foundational phenomenon behind quantum computing.
Let’s begin with a slightly modified example from the celebrated Northern Irish physicist John Stewart Bell:
Alice and Bob know that Prof. Bertlmann always wears mismatched socks. If his left sock is pink, his right sock is certain to not be pink. (Our illustrations are loosely based on Bell’s own cartoons of his friend, Reinhold Bertlmann, which he drew for a 1980 article to explain entanglement.)

Alice and Bob wish to test if Prof. Bertlmann’s choice in socks persists outside the classroom, so they decide to spy on him.
Suppose Alice is standing one block away, and she sees that Prof. Bertlmann’s left sock is blue. Immediately, she knows that Bob—who’s keeping an eye on Bertlmann’s right sock—will see pink. This holds true even if Alice is light-years away from Bertlmann, following all the sartorial goings-on with a telescope. Once she measures the color of one sock, Alice instantaneously knows something about what Bob will measure about the other sock. This is because the pair of mismatched socks are what physicists (and overqualified wardrobe consultants) describe as being correlated with one another.
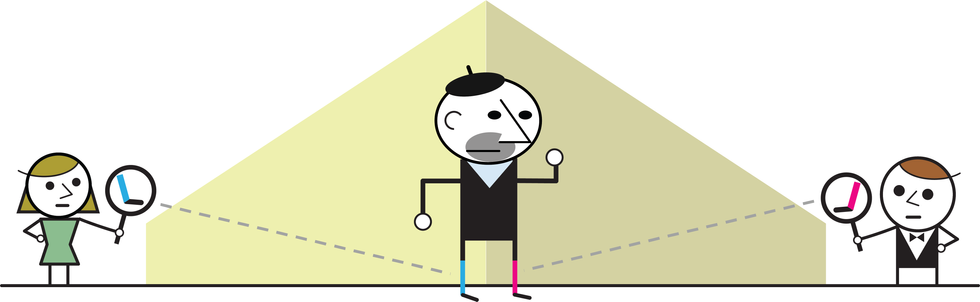
There is no mystery to how this correlation arises: Every morning, Prof. Bertlmann intentionally mismatches his socks. If his left sock is blue, he will pull on a right sock that’s pink. These correlations have three classical characteristics: They are real, local, and deterministic.
Real: The socks have a definite color prior to Alice’s or Bob’s measurement.
Deterministic: The color of the socks is not random. Given exactly the same initial conditions (for example, Tuesday, chance of rain, sore toe), Prof. Bertlmann will put on the mismatched socks the same way. Note: The specific colors worn on each foot may be difficult for Alice and Bob to predict, but the process is not strictly random.
Local: The color of the socks depends only on nearby surroundings—that is, what Bob sees should not depend on Alice’s measurement.
Let us now suppose Prof. Bertlmann wishes to teach his snooping students a thing or two about entanglement. The next morning, he puts on a mismatched pair of quantum socks, whose colors are entangled.
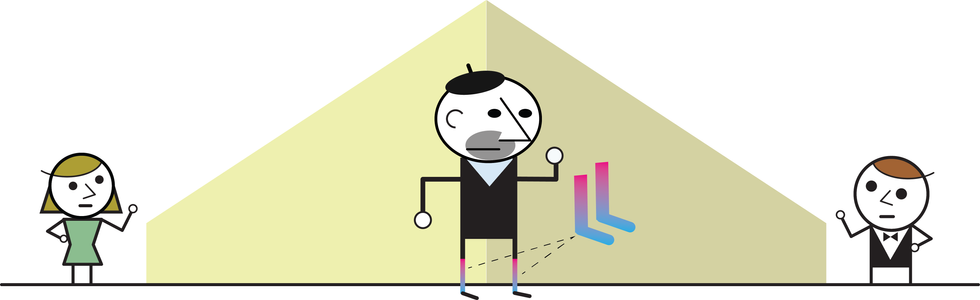
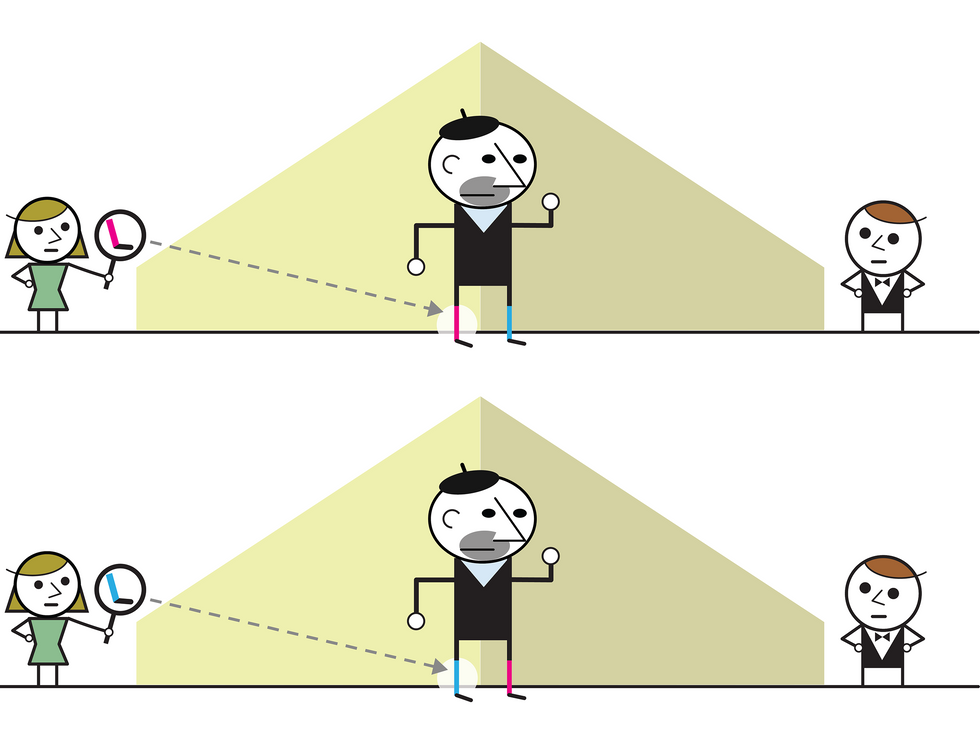
Unlike his classical socks, Prof. Bertlmann’s entangled quantum socks are:
Unreal: The socks have no definite color prior to measurement.
Nondeterministic: The color of the socks is random. Measurements under the exact same initial conditions are unpredictable—for example, 50 percent of the time a sock will be pink, 50 percent of the time it will be blue.
Nonlocal: The color of each sock is dependent on nonlocal surroundings—that is, what Bob sees depends on Alice’s measurement.
In the quantum case, if Alice measures the color of one sock, her measurement instantaneously updates the color of the other sock, which had previously been indefinite. (Note: Because the sock color is random, this does not, strictly speaking, transmit information—and therefore cannot be used for faster-than-light communication.)
But, Alice objects, the socks are close together—couldn’t they send some signal to each other? Is the update really instantaneous? To further convince his students that there is something nonlocal happening, Prof. Bertlmann ships each of the socks to distant stars that are light-years apart from one another.



Then he asks Alice and Bob to perform the same experiment.
Again, what Bob sees depends on Alice’s measurement, even though there is no way for the socks to communicate. This result should be shocking. As Prof. Bertlmann puts it:
“How come they always choose different colors when they are looked at? How does the second sock know what the first has done?”
§
A brief historical detour: Anxiety about entanglement originates from the famous
1935 EPR paper by Albert Einstein, Boris Podolsky, and Nathan Rosen (collectively known as EPR, from their initials). EPR recognized that quantum mechanics specified a world that was nondeterministic and nonlocal, and argued that these properties implied that quantum mechanics is incomplete as a theory. Einstein was particularly concerned about the lack of locality. He famously lamented the instantaneous measurement update between entangled particles as “spukhafte Fernwirkung” (“spooky action at a distance”) because he could not reconcile it with the “ideas of physics.” From Einstein’s letters to Max Born:
“If one asks what… is characteristic of the world of ideas of physics, one is first of all struck by the following: the concepts of physics relate to a real outside world… it is a further characteristic of these physical objects that they are arranged in a space-time continuum. An essential aspect of this arrangement of things in physics is that they lay claim, at a certain time, to an existence independent of one another.”
To preserve these reasonable assumptions—and rescue physics from the seemingly irreconcilable weirdness that quantum mechanics introduced—physicists began playing with “hidden-variable theories.”
According to hidden-variable theory, in Alice and Bob’s experiment the quantum socks are secretly predetermined (by a “hidden” variable) to be one color or another, and it only seems as though Alice’s measurement of the first sock instantaneously updates the color of the other sock. Hidden-variable theories, it was thought, could reproduce all the odd results quantum mechanics predicted without sacrificing local realism.
Here is where we return to the topic of this article—because quantum entanglement lies at the heart of questions about hidden-variable theory.
If hidden-variable theories are correct, entanglement is just an illusion of nonlocality; Bertlmann’s quantum socks would not in that case actually have a strange connection irrespective of distance. But if hidden-variable theories are wrong, entanglement really does link the socks no matter how far apart they are.
Without any way of experimentally differentiating between either theory, physicists relegated the conundrum to the realm of philosophy—until Bell, the Northern Irish physicist referenced earlier, found a solution.
§
Back to the present day, where the skeptical students Alice and Bob are unimpressed by Prof. Bertlmann’s supposedly entangled socks. Again, from their perspective, there is no experimental difference between “spooky” socks and hidden-variable socks, which only appear to update each other upon measurement but whose color (according to hidden-variable theory) would actually be preordained.
To enlighten his mistrustful mentees about the true nature of entanglement, Prof. Bertlmann sets up a new experiment.
In this experiment, Alice and Bob fly off in spaceships. A source shoots out entangled pairs of quantum socks toward them. Alice and Bob each have special detectors with two settings. Alice’s detector can be in setting A or setting a; Bob’s detector can be set to either setting B or setting b. (To pick a setting, they each flip a coin after the socks are sent so there is no way the socks know the settings ahead of time.)

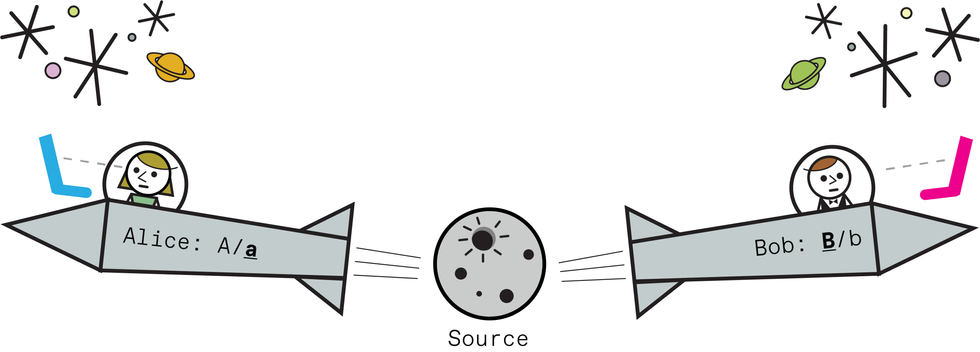
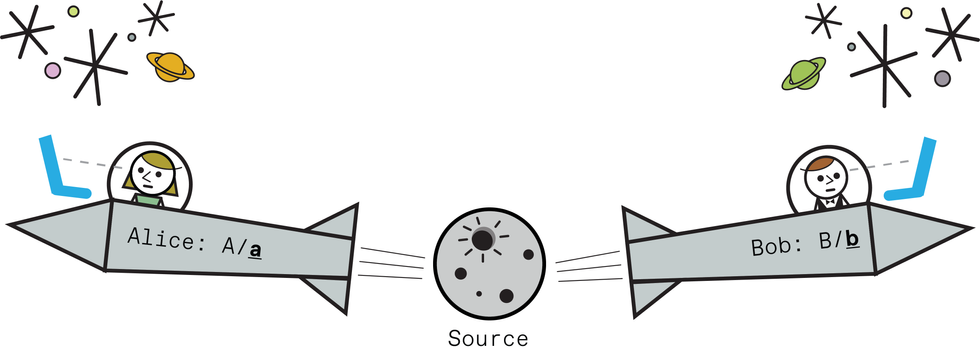
Here is a sample output from Alice and Bob:
| Alice | Bob |
|---|---|
| P | B |
| B | B |
| B | B |
| B | B |
| B | P |
| B | B |
| P | P |
| P | B |
| B | P |
| B | B |
| B | P |
| P | P |
| B | B |
| P | B |
| B | B |
| B | B |
| P | P |
| P | P |
As you can see, the colors Alice and Bob measure are random. Let’s now add the detector settings, which are also random.
Setting | Alice | Setting | Bob |
A | P | b | B |
A | B | B | B |
a | B | b | B |
A | B | B | B |
a | B | B | P |
a | B | b | B |
A | P | B | P |
A | P | b | B |
a | P | B | P |
A | B | B | B |
a | B | B | P |
a | P | b | P |
a | B | b | B |
A | P | b | B |
A | B | B | B |
a | B | B | B |
A | P | b | P |
a | P | B | P |
The table shows that when Alice and Bob use different settings, the socks sometimes match and sometimes mismatch. But if Alice and Bob share a setting (both uppercase or both lowercase), they always match. It’s as if, despite the fact that Alice and Bob flipped coins after the socks were sent, the socks could somehow tell each other when to match across the vast distance. This is very strange—as if the sock color were predetermined!
After Alice and Bob have recorded all their data, they come back to Earth, where Prof. Bertlmann explains that the strange coincidence is not quite enough to reveal the true nature of entanglement. What they need is to measure how correlated the socks are, so Alice and Bob create a new table where pinks are -1 and blues are +1.
Setting | Alice | Setting | Bob | Combined Setting | Sum |
A | -1 | b | +1 | Ab | 0 |
A | +1 | B | +1 | AB | 2 |
a | +1 | b | +1 | ab | 2 |
A | +1 | B | +1 | AB | 2 |
a | +1 | B | -1 | aB | 0 |
a | +1 | b | +1 | ab | 2 |
A | -1 | B | -1 | AB | -2 |
A | -1 | b | +1 | Ab | 0 |
a | -1 | B | -1 | aB | -2 |
A | +1 | B | +1 | AB | 2 |
a | +1 | B | -1 | aB | 0 |
a | -1 | b | -1 | ab | -2 |
a | +1 | b | +1 | ab | 2 |
A | -1 | b | +1 | Ab | 0 |
A | +1 | B | +1 | AB | 2 |
a | +1 | B | +1 | aB | 2 |
A | -1 | b | -1 | Ab | -2 |
a | -1 | B | -1 | aB | -2 |
“There is a very simple proof—that you can check on your own—which states that the absolute value of AB - Ab + aB + ab cannot be greater than 2 if the hidden-variable theory of sock color were true,” Prof. Bertlmann explains.
Counting, Alice and Bob tally up their measurements and find the averages for AB, Ab, aB, and ab:
Then they plug the numbers into the formula and find that the (positive) sum exceeds 2!
Puzzled, they ask Prof. Bertlmann what it means. He responds:
“It is often said that entanglement is the essence of quantum mechanics. This simple mathematical inequality—that the formula based on the experimental results will conditionally yield an answer no greater than 2—is at the heart of entanglement. Neither classical correlations nor the correlations of hidden-variable theories could replicate the measurements you took of my socks. Since your answer is 2.3, which is greater than 2, the only explanation is that the entanglement you measured was a fundamentally quantum-mechanical phenomenon. Therefore, each pair of socks was indeed genuinely entangled. Before you measured them, there was no left sock color or right sock color; they were a single quantum object.”
While no socks have been entangled in the real world (yet), there have been numerous experiments confirming that quantum correlations exceed Bell’s inequality, as above. The first experiments entangled electrons and photons, but in the decades since, scientists have even managed to entangle tiny, nanoscale objects, such as a pair of submicroscopic drums.
§
So, what is entanglement? In our first definition, we said that “entanglement is when multiple objects share a single quantum state.” We can update that definition with what we’ve learned: Entanglement is the amount by which multiple objects share a quantum state. By checking the correlations of our measurements, we can quantify how much entanglement there is between objects. The state of entangled objects cannot be described independently. Prof. Bertlmann’s quantum socks, light-years apart, are not reducible to a left sock color and a right sock color. They remain a pair of indeterminate color until they are disentangled by a measurement.
In a quantum computer, qubits are separated by millimeters, not light-years. But the principle still holds, so an entangled pair really is one quantum object—at least until Alice or Bob takes a measurement.
For Further Reading:
Bertlmann’s Socks and the Nature of Reality (1980)—J.S. Bell’s explanation of his own work remains essential, lucid, and funny.
Is the Moon There When Nobody Looks? Reality and the Quantum Theory (1985)—N. David Mermin reviews the EPR controversy and what Alain Aspect’s 1982 experimental confirmation of Bell’s theorem means.
The Age of Entanglement: When Quantum Physics Was Reborn (2008)—Louisa Gilder’s dramatized retelling of the debates between Einstein, Bohr, and others perceives entanglement from the vantage of a novel.
Schrödinger’s Killer App: Race to Build the World’s First Quantum Computer (2013)—Full of off-color asides, the late Jon Dowling’s book is a rigorous but accessible introduction to the principles underlyingquantum computing. It remains generously free online.
- Quantum Entanglement Meets Superconductivity in Novel ... ›
- Is Math the Key to Quantum Entanglement Protection? - IEEE ... ›
- Researchers Produce Entangled Photons Entirely On-Chip - IEEE Spectrum ›
- Entangled Atoms Lead to Ultra-Precise Quantum Sensors - IEEE Spectrum ›
Dan Garisto is a freelance science journalist who covers physics and other physical sciences. His work has appeared in Scientific American, Physics, Symmetry, Undark, and other outlets.