By Ed Fontes (COMSOL), Henrik Ekström (COMSOL), and Andreas Nyman (Intertek)
Introduction
Lithium-ion batteries have become the most common rechargeable batteries for consumer electronics and automotive applications due to their high energy densities, decent power density, relatively high cell voltages, and low weight-to-volume ratios.
The term lithium-ion battery refers to an entire family of battery chemistries. The common properties of these chemistries are that the negative and the positive electrode materials serve as hosts for lithium ions and that the battery contains a nonaqueous electrolyte.
The increased demand and the pressure for improving battery performance have intensified the need for mathematical modeling. Modeling and simulations allow for the analysis of an almost unlimited number of design parameters and operating conditions at a relatively small cost. Experimental tests are used to provide the necessary validation of the models.
For a battery manufacturer, models and simulations help to improve the materials and the design of the battery system. For device manufacturers, who incorporate batteries into products and devices, modeling allows for understanding and simulating performance at relevant operating conditions.
This paper exemplifies the use of models and simulations through a gallery of examples for performance predictions, thermal management and safety assessment, characterization and state-of-healthy monitoring, as well as for fundamental research and understanding.
The Newman Model
Mathematical models can describe and predict cell voltage and current density during discharge, recharge, transient studies, and also include mechanisms for aging and failure. The influence of different material properties and design parameters can be studied under these conditions.
The work horse for high-fidelity model of lithium-ion batteries is the so-called Newman model. The model is based on the Maxwell-Stefan equations for the transport of ions in concentrated binary electrolytes, which are developed and formulated in a very compact form for the lithium-ion electrolytes. In addition, Newman’s team applied porous electrode theory in combination with lithium intercalation in the porous electrodes to describe the battery electrodes. This theory results in homogeneous electrode models, where the electrode material and the pore electrolyte are treated as one homogenous "slab".
The Newman model has been validated by many scientists and researchers over the years. It has also been further developed and extended by others, for example to account for designs with multiple electrode materials, the formation of a solid electrolyte interface, and alternative electrode kinetics. The original 1D model has later also been formulated by COMSOL for 2D, 2D axi, and 3D.
Performance Models
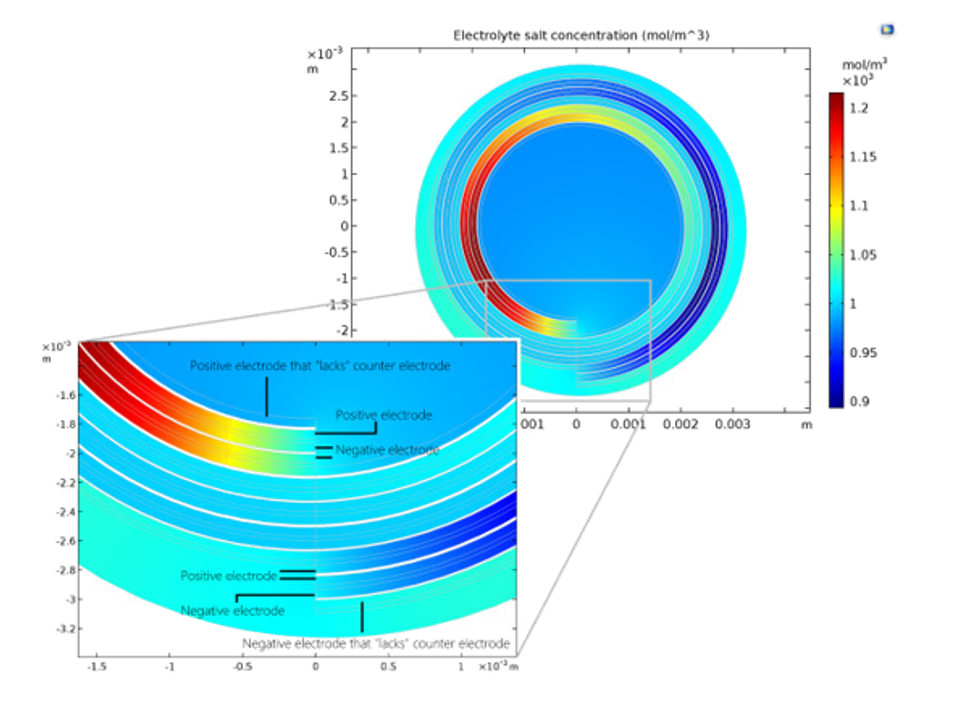
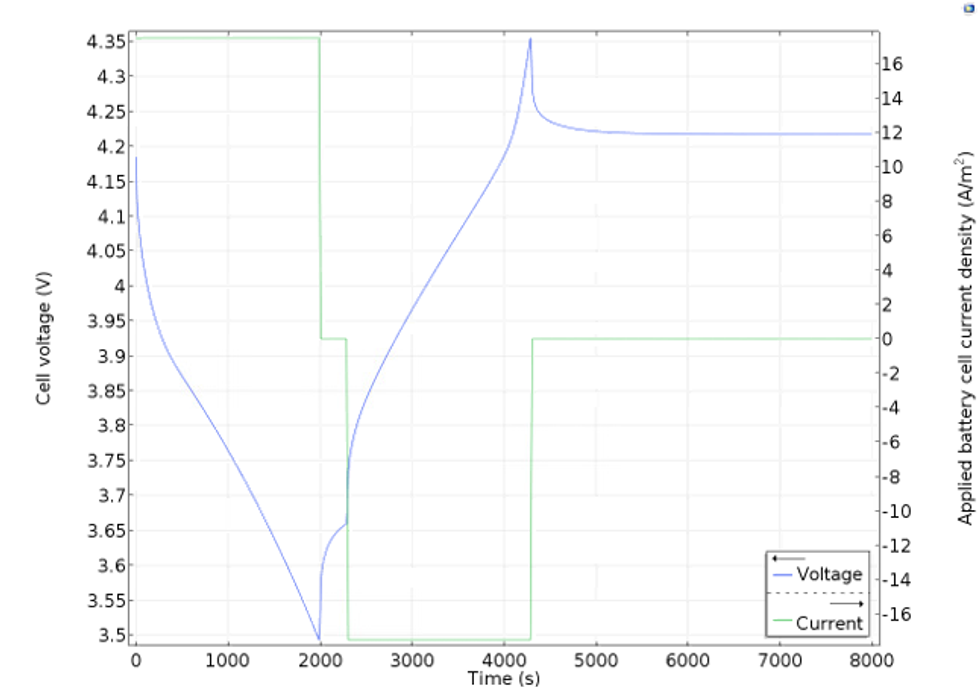
A typical experiment that can be accurately described by a battery model is a discharge-recharge cycle as shown in Figure 2 below. The green line represents the current density. The current density is defined as positive during the initial period of discharge of 2000 seconds, which is then followed by a period of rest (0 current) for 300 seconds. The battery is then recharged (negative current) for 2000 seconds before it is allowed to rest again.
The response of the battery voltage to this cycle is shown by the blue curve and is very accurately predicted by the model. The voltage decays with the discharge time due to losses caused by mass transport resistance, concentration and activation overpotential, and due to thermodynamics. When the battery is allowed to rest for 300 seconds, the voltage recovers slightly as activation and ohmic losses are absent and as concentration gradients are allowed to relax. The battery voltage increases as the battery is recharged, again due to the same losses, but now with opposite sign. When the battery is allowed to rest, the voltage slowly reaches a steady open cell voltage. During operation, the losses mentioned above generate heat.
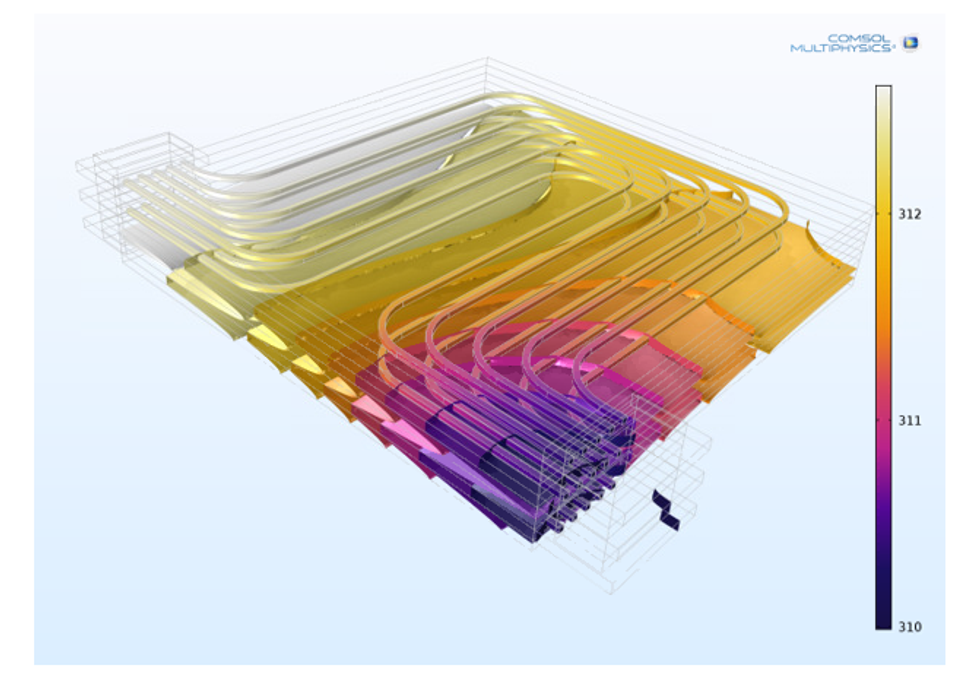
Thermal Management and Safety
The design of the thermal management system in a battery system is substantially complicated by the fact that it has to be able to cope with malfunctioning cells. Malfunction is usually caused by short-circuiting of the electrodes due to metal deposits at the cathode that grow across the electrolyte and make electronic contact with the anode.
Once a short circuit is formed, a very high current density is obtained around the metal dendrite, which causes Joule heating and an increased local temperature. When the temperature is high enough, catalytic combustion of the battery materials leads to thermal runaway of the battery. With improper design, this process ends with fire and may even cause the battery to explode.
Models and simulations allow for testing of different configurations of the cooling system in order to avoid the battery pack to enter thermal runaway, even in the case of short-circuiting.

Heating and cooling design for normal operation and for regular startup is focused on minimizing weight and power consumption. The shape of the cooling channels and the flow rate of the cooling fluid at different operating conditions are usually the factors that are optimized.
Characterization and State of Health (SOH)
It is clear from theory and mathematical models that lithium-ion batteries are highly nonlinear systems where many phenomena are involved at the same time; i.e., electronic current conduction, transport of ions, heterogeneous electrochemical reactions, homogeneous chemical reaction, heat transfer, and fluid flow.
Consequently, there are many factors that influence the performance and it is often difficult to separate the effects of different design and operation parameters on performance. A key to separating the influence of the different involved phenomena is the fact that they often have different time constants. For example, electrochemical reactions are usually pretty fast compared to diffusion. Electronic current conduction is an extremely fast phenomenon that responds immediately to a change in electric potential.
Electrochemical impedance spectroscopy (EIS) can be used to separate the contribution to the losses that the different phenomena are responsible for. For example, a sinusoidal perturbation in potential at high frequencies gives a delayed sinusoidal response in the current due to relatively fast phenomena such as electrode kinetics, since slow phenomena such as diffusion only "see" an average. Conversely, at low frequencies, any delay of the response of the current to a perturbation in potential is due to slow processes, such as diffusion. This is reflected in a complex impedance at different frequencies, giving the contribution of different phenomena and also making it possible to run parametric estimations of the material and electrochemical properties of a cell.
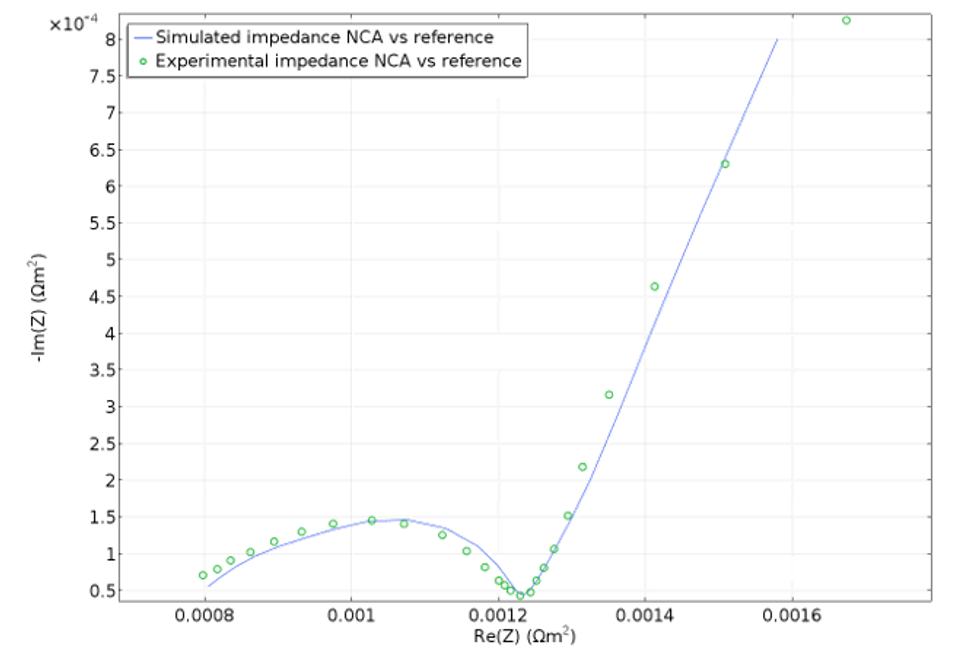
The Newman model has also been expanded to include the simulation of EIS. This model can be used to create and validate simplified lumped models; for example, equivalent circuit models, which may be installed with the battery system for state-of-health monitoring.
Beyond the Newman Model
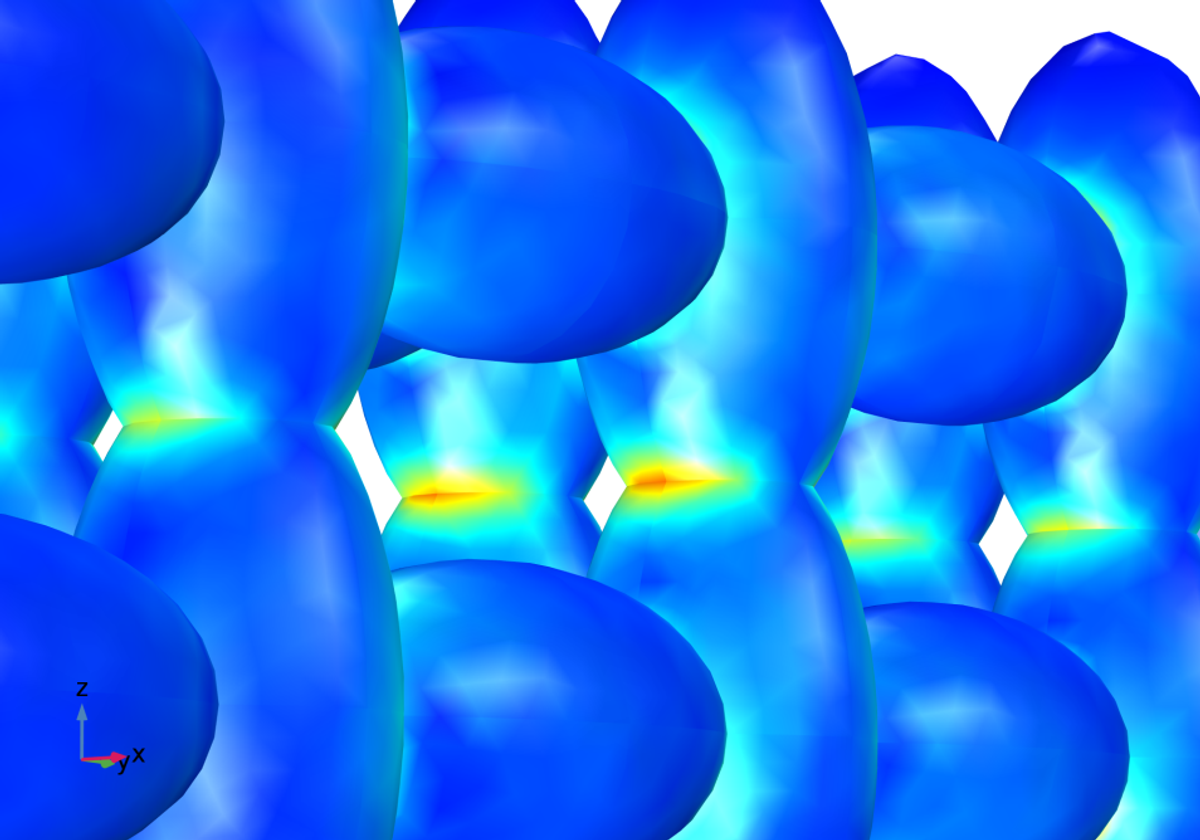
The latest development for understanding the electrodes in batteries is to use heterogeneous models that treat the geometry of the material in detail, in contrast to the homogeneous model. This is achieved by constructing the geometry from micrographs.

The example above shows a hypothetical heterogeneous structure with the graphite particles described as ellipsoids and the pore electrolyte filling the void between the skeleton formed by the ellipsoids. A structural analysis coupled to the detailed electrochemistry, with volume expansion caused by lithium intercalation, reveals that the necks of the skeleton structure are subjected to the highest stresses and strains. Therefore, cracks may form there over repeated cycles and increase the ohmic losses, which contribute to the deterioration of the battery performance.
Multiphysics Models and Partial Differential Equations
The most accurate way of describing the lithium-ion battery is through physics-based models formulated with partial differential equations. Further development of these batteries requires new models and new formulations, such as the heterogeneous model exemplified above. Models must be able to describe the fundamental processes that determine battery performance in order to give the deeper understanding required for developing new materials and new designs. There is no way around this; models and simulations are the shortcuts.
To read the complete white paper, click here.