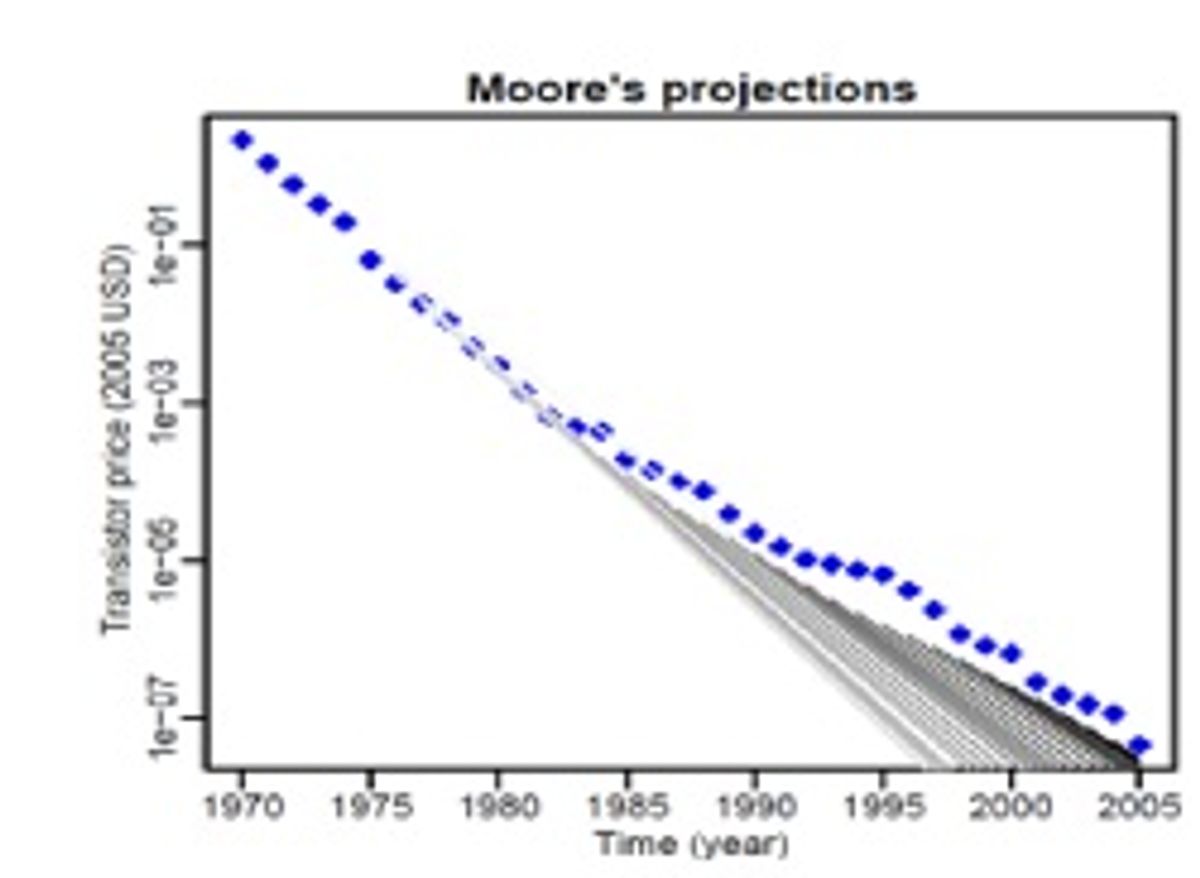
The next time you’re at cocktail party and someone says “Computing power doubles every 18 months,” jump in with this before they can qualify the statement:
“Actually, the 1965 Moore’s Law seems to be a special case of Wright’s Law, spelled out by Theodore P. Wright in a 1936 paper, ‘Factors affecting the costs of airplanes.’ In fact, Wright’s Law seems to describe technological evolution a bit better than Moore’s—not just in electronics, but in dozens of industries.”
Your interlocutors will gaze at you with admiration and wonder. Or, more probably, edge away and leave you in peace.
It turns out that high technology has more in common with low-tech than we thought. The same rules seem to describe price evolution in all 62 areas.
As the analysts point out, “It is not possible to quantify the performance of a technology with a single number. A computer, for example, is characterized by speed, storage capacity, size and cost, as well as other intangible characteristics such as aesthetics. One automobile may be faster while another is less expensive.”
So the analysis focuses on a single variable: cost, specifically the inflation-adjusted price of one “unit.” (A “unit” is itself sometimes a fluid concept in a rapidly changing field. Consider what “one transistor” meant in 1969, and what it meant in 2005.) So, for example, recasting Moore’s Law to translate computing power into unit cost morphed the familiar “computing power doubles every 18 months” into “transistor costs drop by 50 percent every 1.4 years.”
The prediction models evaluated were:
- Moore’s Law (1965). “Time is the teacher.” The cost of a unit decreases exponentially over time. In his 1965 Electronics paper,” Cramming more components onto integrated circuits,” [pdf] Intel co-founder Gordon Moore predicted that—over a ten year span—the number of transistors on a chip would double each year. He reportedly revised the doubling-time to two years, and others later reformulated it into the familiar “Computing power doubles every 18 months.” Like the Mars rovers Spirit and Opportunity, Moore’s Law has continued to operate far past its original design horizon.
- Wright’s Law (1936). “We learn by doing.” The cost of a unit decreases as a function of the cumulative production.
- Goddard’s Law (1982, in IEEE Transactions on Components, Hybrids, and Manufacturing Technology). “Economies of scale.” Unit cost decreases as the scale of production increases.
- Nordhaus’s synthesis (2009): “Time and experience,” combines Moore’s and Wright’s formulations to project unit costs as a function of both time and cumulative production.
- Sinclair, Klepper, and Cohen’s synthesis (2000): “Experience and scale,” combines Wright and Goddard to predict that unit costs fall as a function of both cumulative production and the rate of production.
(The Santa Fe group also included an analysis of Wright’s Law lagged by a year to reflect the latency of the learning curve.)
Proceeding on the assumption that hindsight isn’t always 20/20, the researchers did a pairwise comparison, generating an error score for a model’s performance for every interval in the database. As in a round of golf, the lowest score wins. (The gray lines in the accompanying graphs show two models' predictions from a range of starting dates.)
What did they conclude?
Because time (Moore), annual production (Goddard), and cumulative production (Wright) are clearly interrelated, the methods generate similar forecasts.
The Sinclair, Klepper, Cohen synthesis broke down over long time spans, probably because its extra variables made it prone to overfitting, too sensitive to random noise in the data
Goddard’s Law performed well over short periods but also broke down over decades.
And the winners are: Moore’s Law and Wright’s Law, with Wright ahead by a nose. When production increases exponentially (as it often did in the researchers’ data), Moore’s and Wright’s Laws wind up looking very similar; overall, Wright’s Law came out ahead on the strength of its performance over longer time spans. (Cocktail-party factoid: Ironically, Moore’s Law performed particularly poorly in predicting transistor prices; the rapid increase in chip density and soaring numbers of chips manufactured created a “superexponential” increase in cumulative production that Wright’s Law accommodated better than Moore’s.)
Graphs: Nagy et. al, Santa Fe Institute
Douglas McCormick is a freelance science writer and recovering entrepreneur. He has been chief editor of Nature Biotechnology, Pharmaceutical Technology, and Biotechniques.