Will Silicon Save Quantum Computing?
Silicon has become a leading contender in the hunt for a practical, scalable quantum bit
Grand engineering challenges often require an epic level of patience. That’s certainly true for quantum computing. For a good 20 years now, we’ve known that quantum computers could, in principle, be staggeringly powerful, taking just a few minutes to work out problems that would take an ordinary computer longer than the age of the universe to solve. But the effort to build such machines has barely crossed the starting line. In fact, we’re still trying to identify the best materials for the job.
Today, the leading contenders are all quite exotic: There are superconducting circuits printed from materials such as aluminum and cooled to one-hundredth of a degree above absolute zero, floating ions that are made to hover above chips and are interrogated with lasers, and atoms such as nitrogen trapped in diamond matrices.
These have been used to create modest demonstration systems that employ fewer than a dozen quantum bits to factor small numbers or simulate some of the behaviors of solid-state materials. But nowadays those exotic quantum-processing elements are facing competition from a decidedly mundane material: good old silicon.
Silicon had a fairly slow start as a potential quantum-computing material, but a flurry of recent results has transformed it into a leading contender. Last year, for example, a team based at Simon Fraser University in Burnaby, B.C., Canada, along with researchers in our group at University College London, showed that it’s possible to maintain the state of quantum bits in silicon for a record 39 minutes at room temperature and 3 hours at low temperature. These are eternities by quantum-computing standards—the longevity of other systems is often measured in milliseconds or less—and it’s exactly the kind of stability we need to begin building general-purpose quantum computers on scales large enough to outstrip the capabilities of conventional machines.
As fans of silicon, we are deeply heartened by this news. For 50 years, silicon has enabled steady, rapid progress in conventional computing. That era of steady gains may be coming to a close. But when it comes to building quantum computers, the material’s prospects are only getting brighter. Silicon may prove to have a second act that is at least as dazzling as its first.
What is a quantum computer? Simply put, it’s a system that can store and process information according to the laws of quantum mechanics. In practice, that means the basic computational components—not to mention the way they operate—differ greatly from those we associate with classical forms of computing.
Speeding Up Search
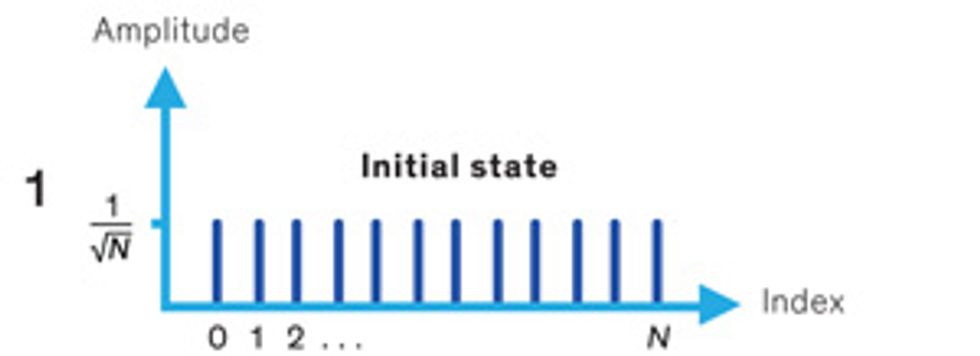
In a classical search algorithm, hunting for a particular string in an unstructured database involves looking at every entry in succession until a match is found. On average, you’d have to run through half, or N/2, of the queries before the correct entry is located. Grover’s algorithm, a quantum search algorithm named for computer scientist Lov Grover, could speed up that work by simultaneously querying all entries. The process still isn’t instantaneous: Finding the correct one would take, on average, √N queries. But it could make a difference for large databases. To search a trillion entries, the scheme would require 0.0002 percent of the number of queries needed in the classical approach. Here’s how it works.
1. The input, a quantum version of the search string, is set up. It contains N different states, one of which is the index of the string you’re looking for. All N states exist in superposition with one another, much like Schrödinger’s cat, which can be both dead and alive at the same time. At this point, if the input is observed, it will collapse into any one of its N component states with a probability of 1/N (the square of the quantum state amplitude shown in the y-axis of the diagram).
2. The input is fed into the database, which has been configured to invert the phase of the correct entry. Here, phase is a quantum attribute. It can’t be directly measured, but it affects how quantum states interact with one another. The correct entry is highlighted in one step, but we can’t see it. The probability of observing the correct state is still the same as that of all the others.
3. To get around this observation problem, a quantum computer can be made to perform a simple operation that would invert all of the amplitudes of the states about their overall mean. Now, when the input is measured, it will be more likely to collapse into the correct answer. But if N is large, this probability will still be quite small.
4. To increase the probability of observing the correct entry, Grover’s algorithm repeats steps 2 and 3 many times. Each time, the correct state will receive a boost. After √N cycles, the probability of observing that state will be very close to 1 (or 100 percent).
For example, as bizarre as it sounds, in the quantum world an object can exist in two different states simultaneously—a phenomenon known as superposition. This means that unlike an ordinary bit, a quantum bit (or qubit) can be placed in a complex state where it is both 0 and 1 at the same time. It’s only when you measure the value of the qubit that it is forced to take on one of those two values.
When a quantum computer performs logical operations, it does so on all possible combinations of qubit states at the same time. This massively parallel approach is often cited as the reason that quantum computers would be very fast. The catch is that often you’re interested in only a subset of those calculations. Measuring the final state of a quantum machine will give you just one answer, at random, that may or may not be the desired solution. The art of writing useful quantum algorithms lies in getting the undesired answers to cancel out so that you are left with a clear solution to your problem.
The only company selling something billed as a “quantum computing” machine is the start-up D-Wave Systems, also based in Burnaby. D-Wave’s approach is a bit of a departure from what researchers typically have in mind when they talk about quantum computing, and there is active debate over the quantum-mechanical nature and the potential of its machines (more on that in a moment).
The quarry for many of us is a universal quantum computer, one capable of running any quantum or classical algorithm. Such a computer won’t be faster than classical computers across the board. But there are certain applications for which it could prove exceedingly useful. One that quickly caught the eye of intelligence agencies is the ability to factor large numbers exponentially faster than the best classical algorithms can. This would make short work of cryptographic codes that are effectively uncrackable by today’s machines. Another promising niche is simulating the behavior of quantum-mechanical systems, such as molecules, at high speed and with great fidelity. This capability could be a big boon for the development of new drugs and materials.
To build a universal quantum computer capable of running these and other quantum algorithms, the first thing you’d need is the basic computing element: the qubit. In principle, nearly any object that behaves according to the laws of quantum physics and can be placed in a superposition of states could be used to make a qubit.
Since quantum behavior is typically most evident at small scales, most natural qubits are tiny objects such as electrons, single atomic nuclei, or photons. Any property that could take on two values, such as the polarization of light or the presence or absence of an electron in a certain spot, could be used to encode quantum information. One of the more practical options is spin. Spin is a rather abstruse property: It reflects a particle’s angular momentum—even though no physical rotation is occurring—and it also reflects the direction of an object’s intrinsic magnetism. In both electrons and atomic nuclei, spin can be made to point up or down so as to represent a 1 or a 0, or it can exist in a superposition of both states.
It’s also possible to make macroscopic qubits out of artificial structures—if they can be cooled to the point where quantum behavior kicks in. One popular structure is the flux qubit, which is made of a current-carrying loop of superconducting wire. These qubits, which can measure in the micrometers, are quantum weirdness writ large: When the state of a flux qubit is in superposition, the current flows in both directions around the loop at the same time.
D-Wave uses qubits based on superconducting loops, although these qubits are wired together to make a computer that operates differently from a universal quantum computer. The company employs an approach called adiabatic quantum computing, in which qubits are set up in an initial state that then “relaxes” into an optimal configuration. Although the approach could potentially be used to speedily solve certain optimization problems, D-Wave’s computers can’t be used to implement an arbitrary algorithm. And the quantum-computing community is still actively debating the extent to which D-Wave’s hardware behaves in a quantum-mechanical fashion and whether it will be able to offer any advantage over systems using the best classical algorithms.
Although large-scale universal quantum computers are still a long way off, we are already getting a good sense of how we’d make one. There are several approaches. The most straightforward one employs a model of computation known as the gate model. It uses a series of “universal gates” to wire up groups of qubits so that they can be made to interact on demand. Unlike conventional chips with hardwired logic circuitry, these gates can be used to configure and reconfigure the relationships between qubits to create different logic operations. Some, such as XOR and NOT, may be familiar, but many won’t be, since they’re performed in a complex space where a quantum state in superposition can take on any one of a continuous range of values. But the basic flow of computation is much the same: The logic gates control how information flows, and the states of the qubits change as the program runs. The result is then read out by observing the system.
Quantum Contender
Photo: Erik Lucero
The stability of superconducting qubits has improved remarkably over the past decade, and they can be entangled with one another with good fidelity through superconducting buses. But the space required is quite large—a qubit can measure in the millimeters when the resonator needed to control it is included. Extremely low temperatures, in the tens of millikelvins, are also needed for optimal operation.
Another, more exotic idea, called the cluster-state model, operates differently. Here, computation is performed by the act of observation alone. You begin by first “entangling” every qubit with its neighbors up front. Entanglement is a quantum-mechanical phenomenon in which two or more particles—electrons, for example—share a quantum state and measuring one particle will influence the behavior of an entangled partner. In the cluster-state approach, the program is actually run by measuring the qubits in a particular order, along particular directions. Some measurements carve out a network of qubits to define the computation, while other measurements drive the information forward through this network. The net result of all these measurements taken together gives the final answer.
For either approach to work, you must find a way to ensure that qubits stay stable long enough for you to perform your computation. By itself, that’s a pretty tall order. Quantum-mechanical states are delicate things, and they can be easily disrupted by small fluctuations in temperature or stray electromagnetic fields. This can lead to significant errors or even quash a calculation in midstream.
On top of all this, if you are to do useful calculations, you must also find a way to scale up your system to hundreds or thousands of qubits. Such scaling wouldn’t have been feasible in the mid-1990s, when the first qubits were made from trapped atoms and ions. Creating even a single qubit was a delicate operation that required elaborate methods and a roomful of equipment at high vacuum. But this has changed in the last few years; now there’s a range of quantum-computing candidates that are proving easier to scale up [see “Quantum Contenders”].
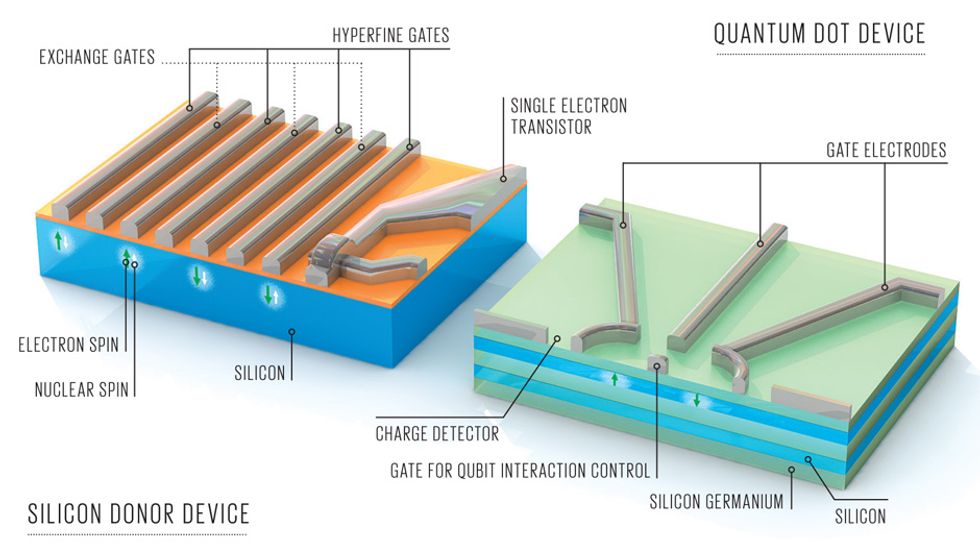
Among these, silicon-based qubits are our favorites. They can be manufactured using conventional semiconductor techniques and promise to be exceptionally stable and compact.
It turns out there are a couple of different ways to make qubits out of silicon. We’ll start with the one that took the early lead: using atoms that have been intentionally placed within silicon.
If this approach sounds familiar, it’s because the semiconductor industry already uses impurities to tune the electronic properties of silicon to make devices such as diodes and transistors. In a process called doping, an atom from a neighboring column of the periodic table is added to silicon, either lending an electron to the surrounding material (acting as a “donor”) or extracting an electron from it (acting as an “acceptor”).
Such dopants alter the overall electronic properties of silicon, but only at temperatures above –220 °C or so (50 degrees above absolute zero). Below that threshold, electrons from donor atoms no longer have enough thermal energy to resist the tug of the positively charged atoms they came from and so return.
This phenomenon, known as carrier freeze-out, describes the point at which most conventional silicon devices stop working. But in 1998, physicist Bruce Kane, now at the University of Maryland, College Park, pointed out that freeze-out could be quite useful for quantum computing. It creates a collection of electrically neutral, relatively isolated atoms that are all fixed in place—a set of naturally stable quantum systems for storing information.
Quantum Contender
Photo: Joint Quantum Institute
Since the ions are made to hover, qubits created in this fashion can be well isolated from stray fields and are thus quite stable. There are some disadvantages to this approach, however. The qubits must be constructed in an ultrahigh vacuum to prevent interactions with other atoms and molecules. And ion qubits must be pushed together to entangle them, which is difficult to do with high precision because of electrical noise.
In this setup, information can be stored in two ways: It can be encoded in the spin state of the donor atom’s nucleus or of its outermost electron. The state of a particle’s spin is very sensitive to changing magnetic fields as well as interactions with nearby particles. Particularly problematic are the spins of other atomic nuclei in the vicinity, which can flip at random, scrambling the state of electron-spin qubits in the material.
But it turns out that these spins are not too much trouble for silicon. Only one of its isotopes—silicon-29—has a nucleus with nonzero spin, and it makes up only 5 percent of the atoms in naturally occurring silicon. As a result, nuclear spin flips are rare, and donor electron spins have a reasonably long lifetime by quantum standards. The spin state of the outer electron of a phosphorus donor, for example, can remain in superposition as long as 0.3 millisecond at 8 kelvins before it’s disrupted.
That’s about the bare minimum for what we’d need for a quantum computer. To compensate for the corruption of a quantum state—and to keep quantum information intact indefinitely—additional long-lived qubits dedicated to identifying and correcting errors must be incorporated for every qubit dedicated to computation. One of the most straightforward ways to do this is to add redundancy, so that each computational qubit actually consists of a group of qubits. Over time, the information in some of these will be corrupted, but the group can be periodically reset to whatever state the majority is in without disturbing this state. If there is enough redundancy and the error rate is below the threshold for “fault tolerance,” the information can be maintained long enough to perform a calculation.
If a qubit lasts for 0.3 ms on average and can be manipulated in 10 nanoseconds using microwave radiation, it means that on average 30,000 gate operations can be performed on it before the qubit state decays. Fault tolerance thresholds vary, but that’s not a very high number. It would mean that a quantum computer would spend nearly all its time correcting the states of qubits and their clones, leaving it little time to run meaningful computations. To reduce the overhead associated with error correction and create a more compact and efficient quantum computer, we must find a way to extend qubit lifetimes.
One way to do that is to use silicon that doesn’t contain any silicon-29 at all. Such silicon is hard to come by. But about 10 years ago, the Avogadro Project, an international collaboration working on the redefinition of the kilogram, happened to be making some in order to create pristine balls of silicon-28 for their measurements. Using a series of centrifuges in Russia, the team acquired silicon that was some 99.995 percent silicon-28 by number, making it one of the purest materials ever produced. A group at Princeton University obtained some of the leftover material and, in 2012, after some careful experimental work, reported donor electron spin lifetimes of more than a second at 1.8 kelvins—a world record for an electron spin in any material. This really showed silicon’s true potential and established it as a serious contender.
Our group has since shown that the spins of some donor atoms—bismuth in particular—can be tuned with an external magnetic field to certain “sweet spots” that are inherently insensitive to magnetic fluctuations. With bismuth, we found that the electron spin states can last for as long as 3 seconds in enriched silicon-28 at even higher temperatures. Crucially, we found lifetimes as high as 0.1 second in natural silicon, which means we should be able to achieve relatively long qubit lifetimes without having to seek out special batches of isotopically pure material.
These sorts of lifetimes are great for electrons, but they pale in comparison to what can be achieved with atomic nuclei. Recent measurements led by a team at Simon Fraser University have shown that the nuclear spin of phosphorus donor atoms can last as long as 3 minutes in silicon at low temperature. Because the nuclear spin interacts with the environment primarily through its electrons, this lifetime increases to 3 hours if the phosphorus’s outermost electron is removed.
Quantum Contender
Photo: Hanson lab/TU Delft
Such diamond qubits are attractive because they interact readily with visible light, which should enable long-range communication and entanglement. The systems can stay stable enough for computation up to room temperature. One challenge researchers must tackle is the precise placement of the nitrogen atoms; this will present an obstacle to making the large arrays needed for full-scale general-purpose quantum computers. To date, researchers have demonstrated they can entangle two qubits. This has been done with two defects in the same diamond crystal and with two defects separated by as much as 3 meters.
Nuclear spins tend to keep their quantum states longer than electron spins because they are magnetically weaker, and thus their interaction with the environment is not as strong. But this stability comes at a price, because it also makes them harder to manipulate. As a result, we expect that quantum computers built from donor atoms might use both nuclei and electrons. Easier-to-manipulate electron spins could be used for computation, and more stable nuclear spins could be deployed as memory elements, to store information in a quantum state between calculations.
The record spin lifetimes mentioned so far were based on measuring ensembles of donors all at once. But a major challenge remained: How do you manipulate and measure the state of just one donor qubit at a time, especially in the presence of thousands or millions of others in a small space? Up until just a few years ago, it wasn’t clear how this could be done. But in 2010, after a decade of intense research and development, a team led by Andrea Morello and Andrew Dzurak at the University of New South Wales, in Sydney, showed it’s possible to control and read out the spin state of a single donor atom’s electron. To do this, they placed a phosphorus donor in close proximity to a device called a metal-oxide-semiconductor single-electron transistor (SET), applied a moderate magnetic field, and lowered the temperature. An electron with spin aligned against the magnetic field has more energy than one whose spin aligns with the field, and this extra energy is enough to eject the electron from the donor atom. Because SETs are extremely sensitive to the charge state of the surrounding environment, this ionization of a dopant atom alters the current of the SET. Since then, the work has been extended to the control and readout of single nuclear spin states as well.
SETs could be one of the key building blocks we need to make functional qubits. But there are still some major obstacles to building a practical quantum computer with this approach. At the moment, an SET must operate at very low temperatures—a fraction of a degree above absolute zero—to be sensitive enough to read a qubit. And while we can use a single device to read out one qubit, we don’t yet have a detailed blueprint for scaling up to large arrays that integrate many such devices on a chip.
There is another approach to making silicon-based qubits that could prove easier to scale. This idea, which emerged from work by physicists David DiVincenzo and Daniel Loss, would make qubits from single electrons trapped inside quantum dots.
In a quantum dot, electrons can be confined so tightly that they’re forced to occupy discrete energy levels, just as they would around an atom. As in a frozen-out donor atom, the spin state of a confined electron can be used as the basis for a qubit.
The basic recipe for building such “artificial atoms” calls for creating an abrupt interface between two different materials. With the right choice of materials, electrons can be made to accumulate in the plane of the interface, where there is lower potential energy. To further restrict an electron from wandering around in the plane, metal gates placed on the surface can repel it so it’s driven to a particular spot where it doesn’t have enough energy to escape.
Large uniform arrays of silicon quantum dots should be easier to fabricate than arrays of donor qubits, because the qubits and any devices needed to connect them or read their states could be made using today’s chipmaking processes.
But this approach to building qubits isn’t quite as far along as the silicon donor work. That’s largely because when the idea for quantum-dot qubits was proposed in 1998, gallium arsenide/gallium aluminum arsenide (GaAs/GaAlAs) heterostructures were the material of choice. The electronic structure of GaAs makes it easy to confine an electron: It can be done in a device that’s about 200 nanometers wide, as opposed to 20 nm in silicon. But although GaAs qubits are easier to make, they’re far from ideal. As it happens, all isotopes of gallium and arsenic possess a nuclear spin. As a result, an electron trapped in a GaAs quantum dot must interact with hundreds of thousands of Ga and As nuclear spins. These interactions cause the spin state of the electron to quickly become scrambled.
Quantum Contender
Photo: Christie Simmons/University of Wisconsin–Madison
Using silicon that has been purified of all but one isotope has helped boost the stability of qubit systems; the material now holds the record for the longest qubit coherence times. Silicon also has an advantage when it comes to fabrication, because systems can be constructed using the tools and infrastructure already put in place by the microelectronics industry. But the small size of quantum dots and, to a greater extent, donor systems will make large-scale integration challenging. While scalable architectures exist on paper, they have yet to be demonstrated. So far, research has largely been restricted to single-dopant systems.
Silicon, with only one isotope that carries nuclear spin, promises quantum-dot qubit lifetimes that are more than a hundred times as long as in GaAs, ultimately approaching seconds. But the material faces challenges of its own. If you model a silicon quantum dot on existing MOS transistor technology, you must trap an electron at the interface between silicon and oxide, and those interfaces have a fairly high number of flaws. These create shallow potential wells that electrons can tunnel between, adding noise to the device and trapping electrons where you don’t want them to be trapped. Even with the decades of experience gained from MOS technology development, building MOS-like quantum dots that trap precisely one electron inside has proven to be a difficult task, a feat that was demonstrated only a few years ago.
As a result, much recent success has been achieved with quantum dots that mix silicon with other materials. Silicon-germanium heterostructures, which create quantum wells by sandwiching silicon between alloys of silicon and germanium and have much lower defect densities at the interface than MOS structures, have been among the front-runners. Earlier this year, for example, a team based at the Kavli Institute of Nanoscience Delft, in the Netherlands, reported that they had made silicon-germanium dots capable of retaining quantum states for 40 microseconds. But MOS isn’t out of the running. Just a few months ago, Andrew Dzurak’s group at the University of New South Wales reported preliminary results suggesting that it had overcome issues of defects at the oxide interfaces. This allowed the group to make MOS quantum dots in isotopically pure silicon-28 with qubit lifetimes of more than a millisecond, which should be long enough for error correction to take up the slack.
As quantum-computing researchers working with silicon, we are in a unique position. We have two possible systems—donors and quantum dots—that could potentially be used to make quantum computers.
Which one will win out? Silicon donor systems—both electron and nuclear spins—have the advantage when it comes to spin lifetime. But embedded as they are in a matrix of silicon, donor atoms will be hard to connect, or entangle, in a well-controlled way, which is one of the key capabilities needed to carry out quantum computations. We might be able to place qubits fairly close together, so that the donor electrons overlap or the donor nuclei can interact magnetically. Or we could envision building a “bus” that allows microwave photons to act as couriers. It will be hard to place donor atoms precisely enough for either of these approaches to work well on large scales, although recent work by Michelle Simmons at the University of New South Wales has shown it is possible to use scanning tunneling microscope tips to place dopants on silicon surfaces with atomic precision.
Silicon quantum dots, which are built with small electrodes that span 20 to 40 nm, should be much easier to build uniformly into large arrays. We can take advantage of the same lithographic techniques used in the chip industry to fabricate the devices as well as the electrodes and other components that would be responsible for shuttling electrons around so they can interact with other qubits.
Given these different strengths, it’s not hard to envision a quantum computer that would use both types of qubits. Quantum dots, which would be easier to fabricate and connect, could be used to make the logic side of the machine. Once a part of the computation is completed, the electron could be nudged toward a donor electron sitting nearby to transfer the result to memory in the donor nucleus.
Of course, silicon must also compete with a range of other exciting potential quantum-computing systems. Just as today’s computers use a mix of silicon, magnetic materials, and optical fibers to compute, store, and communicate, it’s quite possible that tomorrow’s quantum computers will use a mix of very different materials.
We still have a long way to go before silicon can be considered to be on an equal footing with other quantum-computing systems. But this isn’t the first time silicon has played catch-up. After all, lead sulfide and germanium were used to make semiconducting devices before high-purity silicon and CMOS technology came along. So far, we have every reason to think that silicon will survive the next big computational leap, from the classical to the quantum age.
This article originally appeared in print as “Silicon’s Second Act.”
About the Authors
Nanoelectronics professor John J.L. Morton and research fellow Cheuk Chi Lo investigate silicon-based quantum computing at University College London. Recent worldwide advances in this area have been staggering, Morton says. “Quantum bits now live longer than the time it takes to make a cup of tea, and you can watch the telltale signal on an oscilloscope of a single quantum bit flipping back and forth,” he says. “It’s an exciting time to be working in silicon.”