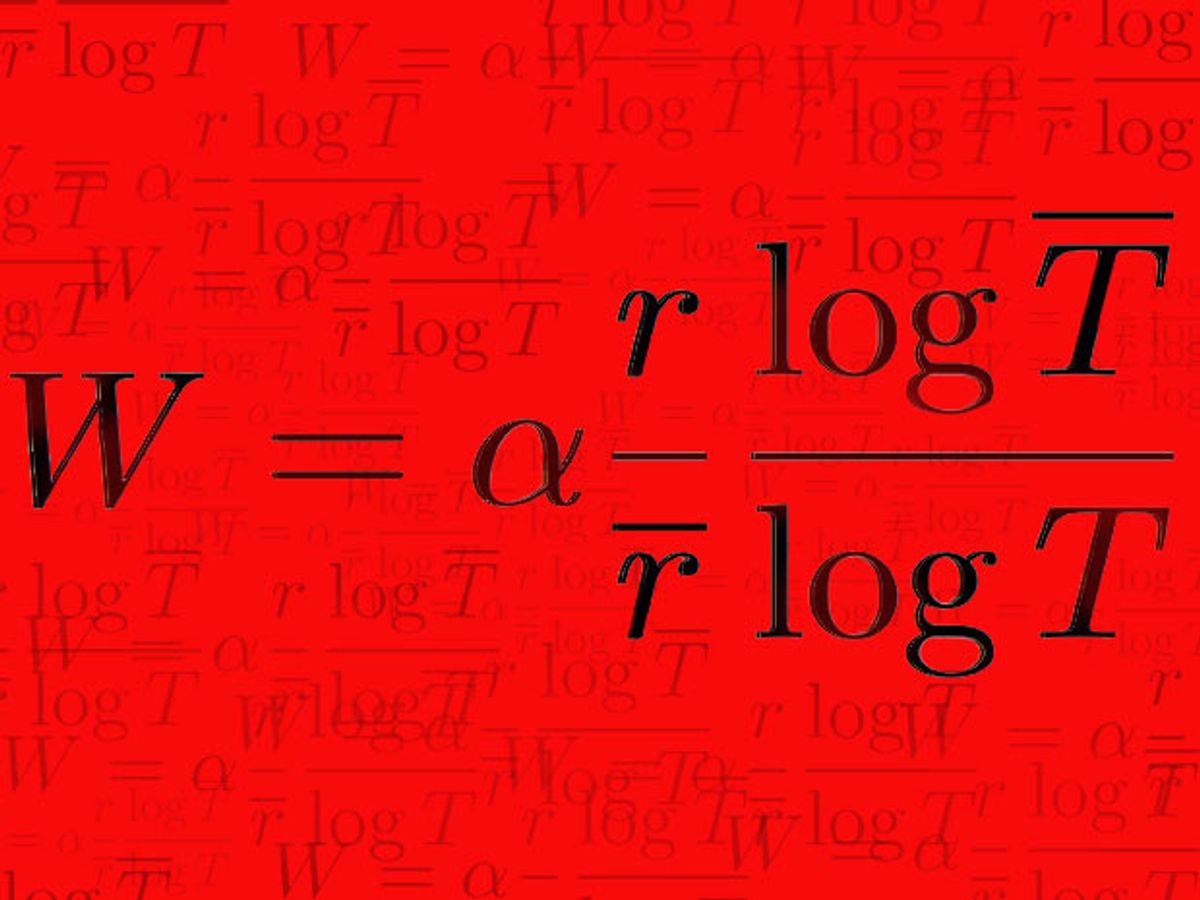The first season of HBO’s “Silicon Valley” was all about the Weissman Score. Vying teams of compression experts used this made-for-TV metric designed to judge the success of compression algorithms.
During the second season, the TV show’s spotlight turned away from compression scores to business drama, as funding and power moved from player to player. But, off screen, the Weissman Score migrated to the real world, where a few professors tested it in papers and in classes. What’s happened since?
“People are indeed using it, but are trying to obfuscate its origins,” says Tsachy Weissman, the Stanford professor who, along with electrical engineering graduate student Vinith Misra, came up with the algorithm at the request of a technical advisor to the show. “They do that because they want to be taken seriously.”
It has certainly become easier to use since it first appeared on the show in 2014; GitHub and other open source code repositories offer downloadable scripts to allow developers to quickly generate Weissman scores for their code.
The first known Weissman score early adopters aren’t currently using the metric, however. Marcelo Weinberger, a distinguished scientist at the University of California at Berkeley, is no longer teaching information theory.
Jerry Gibson, a professor at the University of California at Santa Barbara, has offered it up to students to use in a final course project without telling the students where the formula came from; the one student who has taken him up on it used it to compare two different data compression schemes, in the same way it was used in the show.
The score has some issues, Gibson says. “It just includes the log of the time to compress as a factor in comparing compression algorithms in addition to the compression ratio, so more complicated schemes will be penalized.” Also, he says, “it is necessary to choose a common platform for the compression methods to use, and that choice can impact the final results.” Finally, he points out, the score, as used in the TV show, is misleading, “since the Weissman score implies lossless compression, which is never considered seriously for any video appplications since a much lower rate can be achieved by allowing losses that the human cannot perceive.”
As for why Gibson didn’t mention that the score came from the show, he says that he wanted the students to take the measure seriously, but it turned out that the student who did use it was indeed familiar with it from the show.
Dror Baron, an assistant professor of electrical and computer engineering at North Carolina State University, was planning to use it to replace scattergraphs in a paper he had written, but the paper was too far along in the review process to do so. He also has some concerns about what he sees as a minor weakness in the algorithm: its failure to define units. He's encouraging Weissman to fix this issue.
Baron explains as an example:
The score contains a term log(overbar(T))/log(T), where T and overbar(T) are runtimes for two algorithms. Let's look at the ratio in three ways:
1. If the time units are 60 seconds and 30 seconds, respectively, then log(overbar(T))/log(T) = log(60)/log(30)=1.204.
2. If the units are minutes, then T=0.5, overbar(T)=1, and log(overbar(T))/log(T) = log(1)/log(0.5) = 0.
3. If the units are hours, then log(overbar(T))/log(T) = log(1/60)/log(1/120) = 0.8552.
You can see that varying the units gives pretty different results, which could be messy.”
Baron still believes, though, that “the score gets to the heart of the matter” of compression algorithms.
Correction made in units 26 April 2017.
Tekla S. Perry is a senior editor at IEEE Spectrum. Based in Palo Alto, Calif., she's been covering the people, companies, and technology that make Silicon Valley a special place for more than 40 years. An IEEE member, she holds a bachelor's degree in journalism from Michigan State University.