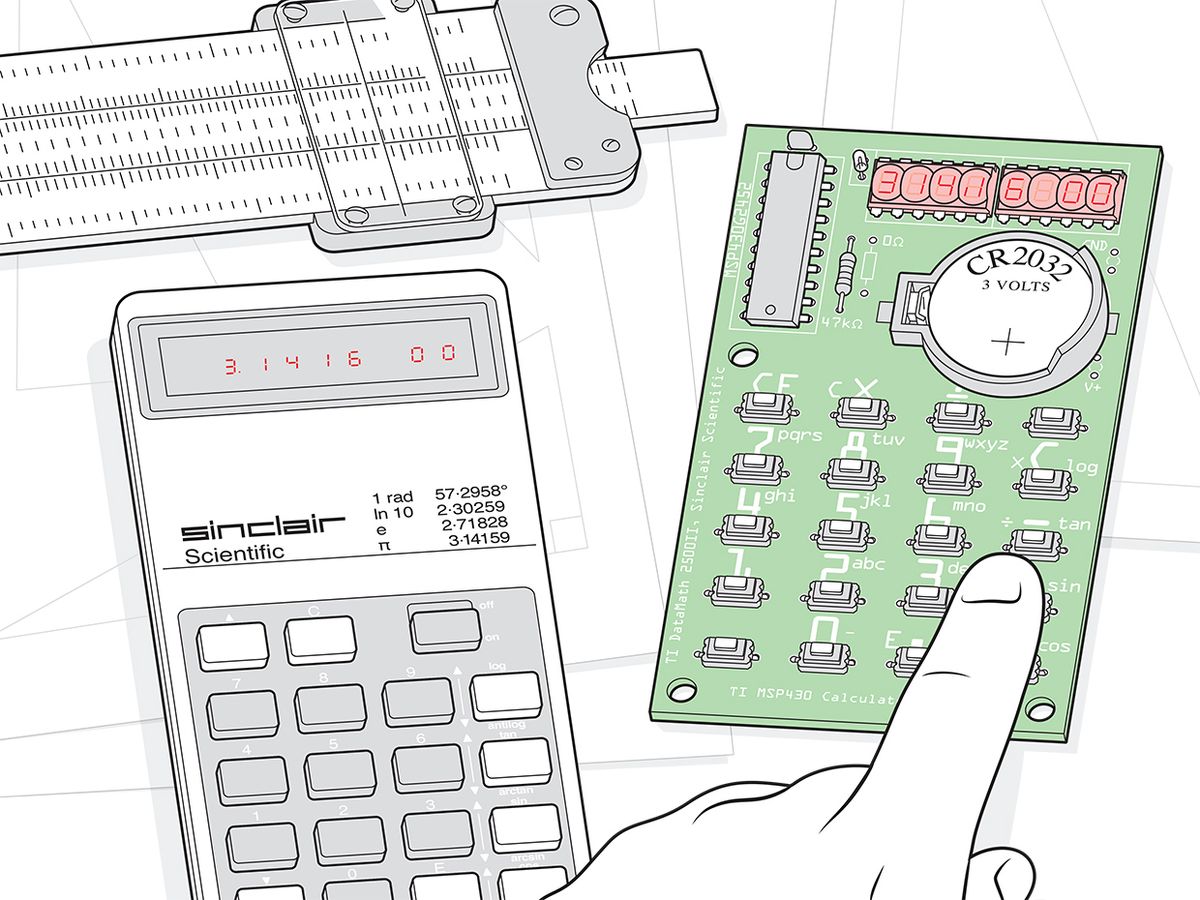
Was the Sinclair Scientific calculator elegant? It certainly was a hit, gracing the cover of publications like Popular Mechanics after its release in 1974. Cleverly written firmware dragooned its limited processor, intended only for basic arithmetic, into performing way beyond specifications. This allowed Sinclair to sell a scientific calculator to countless folks who otherwise could not have afforded one. But it was also slow and sometimes inaccurate, provided barely enough mathematical functions to qualify as a scientific calculator, and was difficult for the uninitiated to use.
I’d vaguely known of this calculator because of its place as a milestone toward the birth of the British microcomputer industry and such beloved machines as the Sinclair ZX Spectrum. So I clicked when I came across Chris Chung’s replica kit of the calculator on the Tindie marketplace. Then I read the description of how the original calculator worked—scientific notion only? no “equals” button?—and how the replica reproduced its behavior, by using an emulator running firmware that had been reverse engineered by visually examining the metal of an original processor. This I had to try.
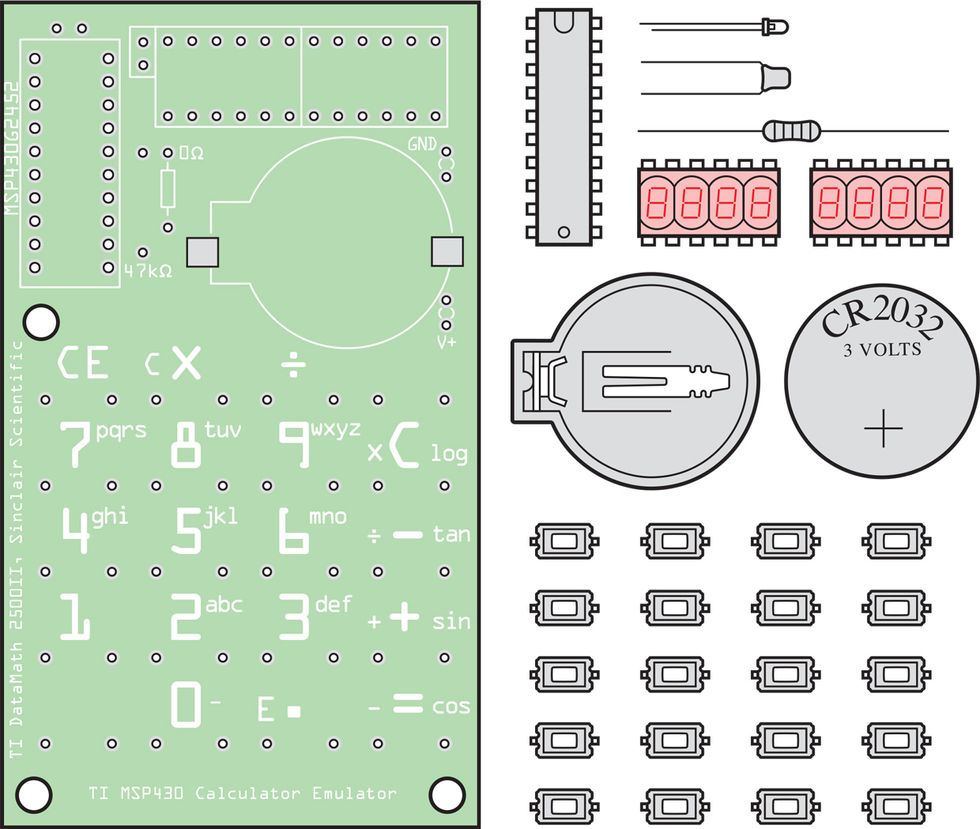
Let’s first get to the hardware. The kit is one of a number of Sinclair calculator replicas, but it wins points for simplicity: One chip and a credit-card-size printed circuit board are combined with a small handful of discrete components. Chung actually offers two kits: his original, developed in 2014 but put on Tindie in late 2019, displays numbers using two small QDSP-6064 bubble LED modules [PDF], which have the classic look of 1970s calculators but are long discontinued and hard to get. His 2020 update of the kit uses modern seven-segment LED displays. The difference in rarity is reflected in the price: The 2020 version costs US $39, while the original version costs $79. However, in a nice touch, the original version lets you have your cake and eat it with regard to the bubble LEDs: The through holes in the PCB are sized to create a friction fit. This means you don’t have to solder in the modules, preserving them for some future project.
Both versions are functionally identical, based around a MSP430 microcontroller. The MSP430 eliminates the need for most of the other components found in the Sinclair Scientific, and runs an emulator of the TMS080x family of chips. The TMS080x family was built by Texas Instruments (TI), and specific versions, like the TMS0805 used in the Sinclair Scientific, were differentiated by the contents of the chip’s 3,520-bit ROM.
For many years, how Sinclair coaxed this chip into performing magic remained locked away in TMS0805 chip ROMs. That began to change in 2013, when Ken Shirriff got wind of the Sinclair Scientific after getting involved with the Visual 6502 team. This group likes to reverse engineer classic chips, for which the original design drawings are often lost. Sometimes this involves etching chip packages away with acid and carefully photographing the exposed silicon dies with a microscope to see the individual transistors. Shirriff was able to create a generic simulator of a TMS080x chip in JavaScript just by studying Texas Instruments’ patent filings, but the specific code used in the Sinclair’s TMS0805’s ROM still eluded him, until Visual 6502 team member John McMaster took photographs of an exposed die in 2014.
Shirriff is no stranger to IEEE Spectrum due to his extensive work in the history of computing, so I emailed him to ask how he’d gone from a micrograph to working code. By looking at how the metal oxide gates were laid down in the ROM section of the chip, “I was able to extract the raw bits the same day,” Shirriff wrote back. “Phil Mainwaring, Ed Spittles, and I spent another day figuring out how the raw bits corresponded to the code….The code was 320 words of 11 bits, but the ROM was physically 55 rows and 64 columns.…Through a combination of examining the circuitry, analyzing patterns in the bits, and brute-force trying a bunch of combinations, we figured out the arrangement and could extract the code.”
Once he had the code loaded into his simulator, Shirriff could tease out its workings. The algorithms used throughout “were essentially the simplest brute-force algorithms that could get an answer. But there were some interesting mathematical tricks they used to get more accuracy, not to mention programming tricks to get the code to fit,” he explained. (If you want detailed explanations, Shirriff maintains an online version of his simulator that lets you step through the code, line by line.)
The Sinclair Scientific was able to reduce complexity by using reverse Polish notation, in which mathematical operators come after the numbers they are operating on—for instance, “5 + 4 =” becomes “5 4 +.” The trigonometric functions used an iterated approximation technique that could take several seconds to produce results and were often accurate only to the first three significant figures. The calculator also used fixed scientific notation for everything—there was no way to enter a decimal point. So rather than entering “521.4,” you’d enter “5214,” which is displayed as “5.214”; then you’d press “E” and enter “2,” making the number “5.214 x 102.” Only one number could be entered at a time.
On paper this looks terrible, something you’d have used only if you couldn’t afford, say, the HP-35, whose designers prided themselves on accuracy and functionality (although the HP-35 also used reverse Polish notation, it did so in a more sophisticated way).
But Sinclair wasn’t trying to compete against other calculators; he was competing against slide rules. I’d read that point in histories before, but I didn’t really understand its meaning until I held this kit in my hand. By chance, I’d also recently purchased a vintage Pickett slide rule and learned how to do basic operations with it, thanks to the lessons available on the International Slide Rule Museum website. As I used the Sinclair Scientific, I was struck by how conceptually similar it was to using my slide rule. There, two- to three-figure accuracy is the norm, the rule’s sliding “cursor” means you’re passing just one number between scales, and you typically don’t bother about magnitudes—you work with the most significant figures and make a mental estimate to insert the decimal point at the end, so that 52 x 2 and 5,200 x 20 are calculated in exactly the same way.
This realization is why I feel replica kits are so important—they are an easy way to provide the understanding that only comes from operating a device with your own hands. It was a great reminder that, as folks like Henry Petroski have pointed out, good design is not really something that exists as an abstract ideal but as something that exists only within a specific context. So, was the Sinclair Scientific elegant? For me, the answer is a resounding yes.
This article appears in the June 2020 print issue as “The Sinclair Scientific, Remade.”
Stephen Cass is the special projects editor at IEEE Spectrum. He currently helms Spectrum's Hands On column, and is also responsible for interactive projects such as the Top Programming Languages app. He has a bachelor's degree in experimental physics from Trinity College Dublin.