The Future of Cybersecurity Is the Quantum Random Number Generator
Truly random numbers will provide an unbreakable tool set for cryptography

In 1882, a banker in Sacramento, Calif., named Frank Miller developed an absolutely unbreakable encryption method. Nearly 140 years later, cryptographers have yet to come up with something better.
Miller had learned about cryptography while serving as a military investigator during the U.S. Civil War. Sometime later, he grew interested in telegraphy and especially the challenge of preventing fraud by wire—a problem that was frustrating many bankers at the time. As a contemporary, Robert Slater, the secretary of the French Atlantic Telegraph Co., wrote in his 1870 book Telegraphic Code, to Ensure Secresy [sic] in the Transmission of Telegrams, “Nothing then is easier for a dishonest cable operator than the commission of a fraud of gigantic extent.”
In his own book on telegraphic code, published in 1882, Miller proposed encrypting messages by shifting each letter in the message by a random number of places, resulting in a string of gibberish. For example, to encode the word HELP, you might shift the H by 5 so that it became an M, the E by 3 so that it became an H, the L by 2 so that it became an N, and the P by 4 so that it became a T. Even a meddlesome cable operator wouldn’t know what to make of MHNT unless he also had the list of random numbers, 5-3-2-4. For truly unbreakable encryption, each string of random numbers would encode only one message before being discarded.
About 35 years after Miller’s book, Bell Labs engineer Gilbert S. Vernam and U.S. Army Capt. Joseph Mauborgne came out with essentially the same idea, which they called the one-time pad. And ever since, cryptographers have tried to devise a way to generate and distribute the unique and truly random numbers that the technique requires. That, it turns out, is incredibly hard to do.
So instead, we’ve relied on less secure encryption methods, with the consequence that attackers who are sufficiently patient and knowledgeable can now crack into any encrypted data they want. And compared with Miller’s day, today we have more ways of connecting than the telegraph—through Internet of Things devices, wearable tech, and blockchain-dependent services, to name just a few—and they all need strong encryption. According to the 2017 “Cyber Incident & Breach Trends Report” [PDF] by the Online Trust Alliance, more than 150,000 businesses and government institutions were the victims of cybercrime last year. In just one of those attacks, on the consumer credit reporting company Equifax, hackers culled the personal information of nearly 148 million customers. “Surprising no one, 2017 marked another ‘worst year ever’ in personal data breaches and cyber incidents around the world,” the report concluded.
Fortunately, researchers have made good progress in recent years in developing technologies that can generate and distribute truly random numbers. By measuring the unpredictable attributes of subatomic particles, these devices can use the rules of quantum mechanics to encrypt messages. And that means we’re finally getting close to solving one of cryptography’s biggest puzzles and realizing the unbreakable encryption envisioned by Miller so many years ago.
One-Time Pad Encryption
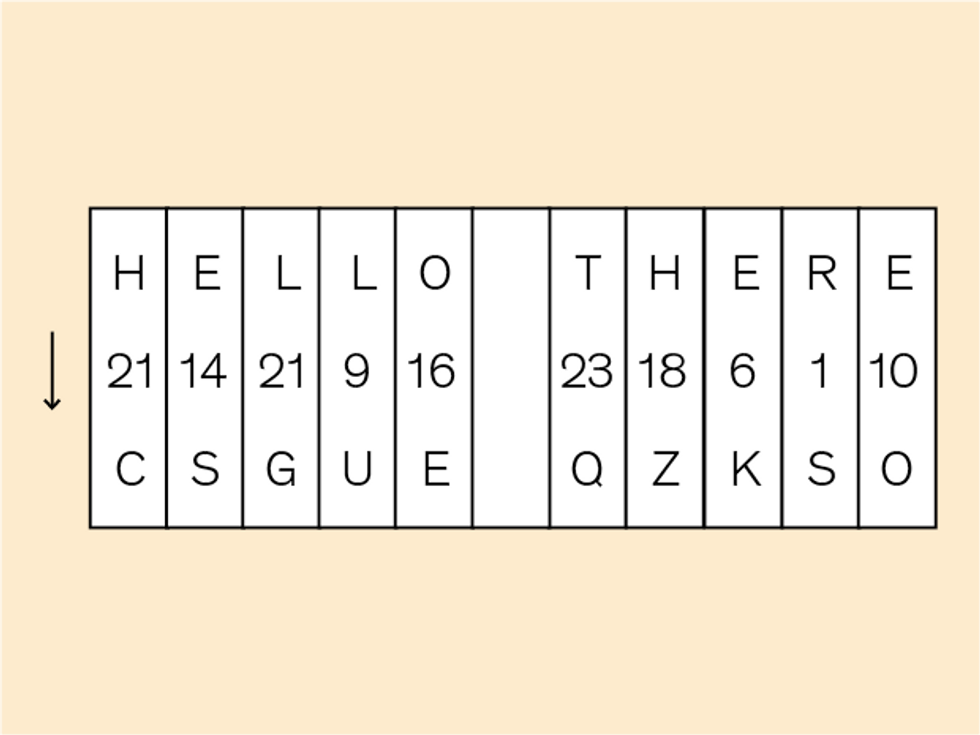
As any cryptographer knows, you need three ingredients to make a hackproof encryption method. First, you need an algorithm that converts your message into a string of meaningless characters. Second, you need a way to produce random numbers. And finally, you need the means to deliver the first two ingredients to the intended recipient without anyone else gaining access.
You cannot protect a message with the first ingredient alone, no matter how good the algorithm is. An encrypted message will be completely exposed to anyone who knows the algorithm used to secure it. That’s why we combine the algorithm with random numbers. Despite its relatively simple algorithm, the one-time pad becomes unbreakable with the addition of random numbers. To recover the original message, you need to know the specific sequence of random numbers the algorithm used to encrypt the message. Those random numbers are a cryptographic key, which unlocks the content of the encrypted message, but it’s useless for deciphering other messages, just as your house key opens your front door but not your neighbor’s. Your encryption system is thus only as strong as your cryptographic key is unpredictable.
Unfortunately, most sources of random numbers aren’t truly random. These pseudorandom-number generators use algorithms to produce sequences of numbers that look random. But again, if you know the underlying algorithm, they become completely predictable.
We can also generate random numbers by measuring physical processes, like flipping a coin or the interference of radio communications on an electric current. One problem with this approach is that if the process is bound by the laws of classical physics, the measurements can be predicted. To be sure, it may take some doing to reverse engineer what’s being measured, but a cryptographer has to assume that somebody will eventually find a way to do so.
Many physical random number sources are also slow. One common method is to record the coordinates of mouse clicks or movements on a computer screen. KeePass, an open-source password manager, uses mouse jiggles to generate a master password. Think how much random clicking or jiggling it would entail just to encrypt every email you wanted to send.
What’s needed, then, is a source of true randomness that is fast enough and that any device can use. That’s where quantum mechanics comes in.
By their nature, subatomic particles like electrons and photons behave in ways that can’t be predicted. If you take two photons emitted by the same atom at different times but under the same conditions, they may exhibit different behaviors, and there’s no way to predict those behaviors ahead of time. That’s not to say any behavior is possible, but of the outcomes that are possible, we can’t predict which one we’ll get. That unpredictability is crucial for developing a random number generator.
One-Way Functions
In the 1990s, a team at the U.K. Ministry of Defence became the first to propose a way to use quantum mechanics for random number generation. Today, you can buy commercial quantum random number generators from companies like QuintessenceLabs and ID Quantique. QuintessenceLabs’ generators are based on quantum tunneling, which occurs when subatomic particles spontaneously pass through a barrier that according to classical physics they shouldn’t be able to cross. The ID Quantique generator tracks the distribution of individual photons as they hit a detector.
All of the available commercial generators are limited to specialized applications, such as encrypting classified military data or financial transactions. They’re much too large, or too slow, or too expensive for mass market use. Imagine instead having a tiny quantum random number generator installed in your phone, your laptop, or anything else that needs to communicate securely. Creating such cheap, compact, and quick quantum systems has been the focus of our group’s research at the Institute of Photonic Sciences, or ICFO, in Barcelona, for the past eight years.
One of the most promising approaches is based on a type of semiconductor laser called a distributed feedback laser diode. We start by oscillating the laser diode above and below its threshold level—that is, the energy level at which the stimulated emission of photons starts. For our laser diodes, the threshold is about 10 milliamperes. Each time the laser exceeds its threshold level, the laser will emit photons with a random phase, which means that the photons will be at an unpredictable point along their wavelength. Those random phases become the basis for the random numbers we use to generate a cryptographic key.
We’ve already built several devices that have helped confirm the “spooky action at a distance” principle in quantum mechanics, which is the idea that entangled particles can interact with one another instantaneously regardless of distance. Specifically, our devices provided an observer-independent method of verifying that the spooky action could occur, which is important when it comes to proving that the instantaneous interaction is actually occurring. We built those devices using fiber optic cable, and each was about the size of a shoebox. Now, using standard chip-fabrication techniques, we’ve integrated the components for our quantum random number source onto an indium phosphide chip measuring less than 2 by 5 millimeters. This chip can be installed directly into a phone or an IoT sensor.
RSA Algorithms
Quside Technologies, a company spun off from our institute last year, is commercializing components using our technology. (One of us, Abellán, is now Quside’s CEO.) Quside’s latest generation of quantum sources can produce several gigabits of random numbers per second, which means one source should be enough for any current or emerging encryption need. And because they can be made using standard chip-fabrication techniques, it should be easy to manufacture them in large volumes.
What’s more, our chips are immune to nearby electronic interference. Generally speaking, any electronic device may be susceptible to thermal or electronic interference. White noise, for example, can interfere with the reception of radio signals. Quantum sources, being so tiny, are especially susceptible, so in most cases, their designers need to pay close attention to eliminate any effects that might corrupt the pure, inherent randomness from the quantum process. Our solution neatly avoids this problem simply because a photon’s phase is largely unaffected by electrical currents in the vicinity.
Another good quantum source for random numbers is light-emitting diodes. In 2015, researchers at the Vienna University of Technology demonstrated the first such compact random number generator. It consists of a silicon-based LED that emits photons in the near infrared and a single-photon detector. Its random number generation was linked to when the photons arrive at the detector. The lab prototype generated random numbers at a rate of a few megabits per second.

A year later, our group in Barcelona demonstrated the chip-based quantum source we mentioned before, that is capable of producing gigabits of random numbers per second using distributed feedback lasers. As a bonus, our sources are built from off-the-shelf components and rely on standard optical communication and manufacturing techniques.
Meanwhile, researchers at SK Telecom [PDF], one of the largest telecom providers in South Korea, have demonstrated a random number generator chip that uses a smartphone camera to detect the fluctuations in an LED’s light intensity. The design was based on a patent from ID Quantique. The prototype, unveiled in 2016, measured 5 by 5 mm; since then SK Telecom has announced plans for a commercial version that’s about the same size—that is, small enough to fit inside your smartphone.
Other researchers are investigating quantum random number generators based on single-photon detection arrays. The arrays can detect the small variations as a light source fluctuates and should provide even better detection of quantum fluctuations than a traditional camera can.
Having an encryption algorithm paired with truly random numbers isn’t enough. You still need a secure way to send your message along with the cryptographic key to the recipient.
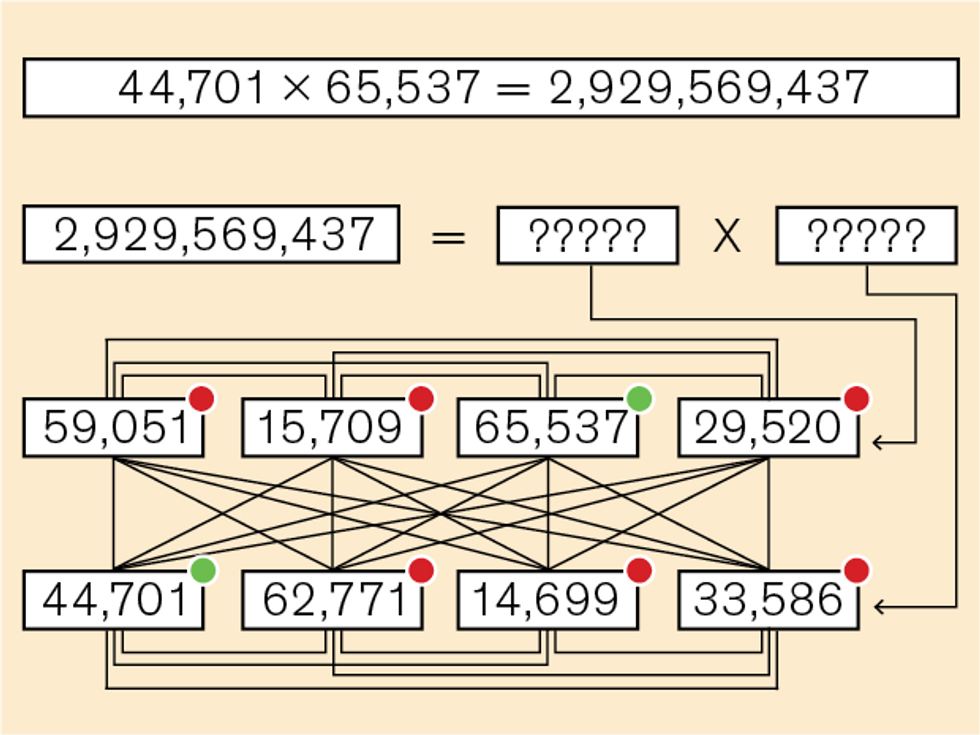
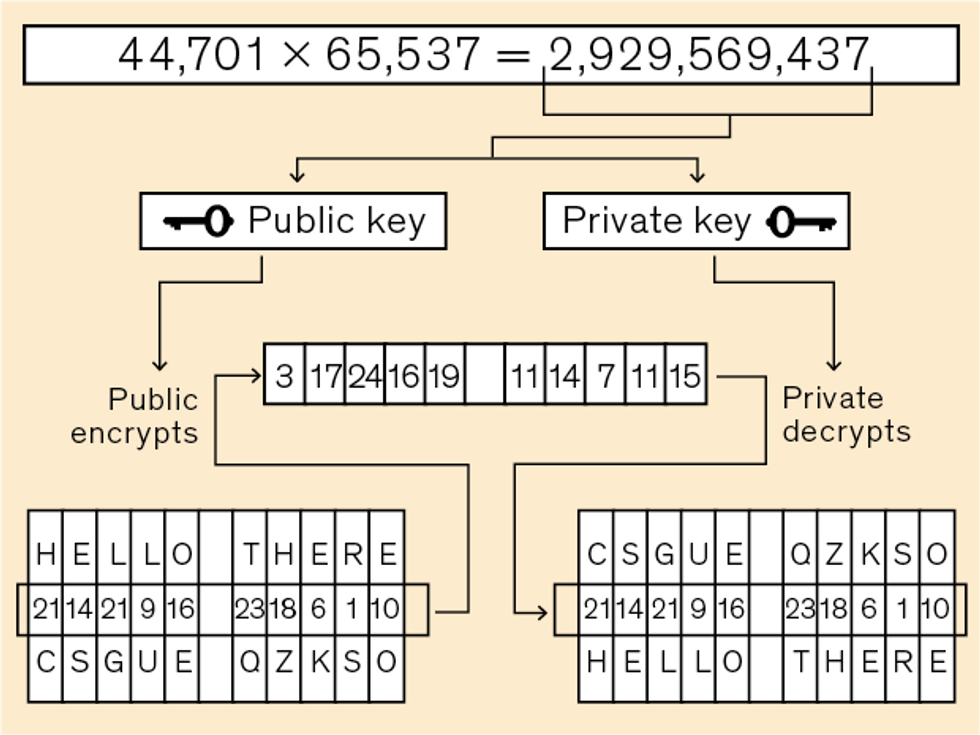
For encrypting and decrypting keys, the standard protocol for many years has been the RSA algorithm. Developed in 1977 by cryptographers Ron Rivest and Adi Shamir and computer scientist Leonard Adleman, it hinges on a mathematical trick known as a one-way function—that’s any calculation that is very easy to solve in one direction but extremely hard to solve in reverse. A classic example—and the one that Rivest, Shamir, and Adleman used—is to multiply two large prime numbers, typically 1,024 or even 2,048 bits in length. It’s of course very easy to multiply the numbers together, but it’s very hard to factor the result back to the original prime numbers.
RSA and similar algorithms give every network user two keys: a public key (known to everyone) and a private key (known only to the user). To send information, you encrypt it using the recipient’s public key. The recipient then decrypts the information using her private key. The algorithms have worked remarkably well for more than four decades because it’s extremely hard to crack the private key, even knowing the public key.

The algorithms aren’t perfect, however. One of the main problems is that they take a long time to encrypt and decrypt a relatively small amount of data. For that reason, we use these algorithms to encrypt keys but not messages. The other big problem is that the algorithms are crackable, at least in theory. Right now, the only methods to crack the code take too long, provided a mathematical breakthrough doesn’t make RSA and similar algorithms easily solvable. For any practical attack, not even today’s supercomputers are up to the task.
Using a clever 20-year-old algorithm, a quantum computer, however, could easily calculate prime number factors by exploiting the quantum property of superposition to drastically decrease the computation time needed to find the correct factors. Today’s quantum computers aren’t powerful enough to handle an RSA-level hack. But it’s only a matter of time, and when that day comes, our current cybersecurity infrastructure will become obsolete.
Ideally, we should be able to exchange cryptographic keys that cannot be cracked before quantum computers or mathematical breakthroughs catch us by surprise. One possibility is to use a technology called quantum key distribution. Much like generating truly random numbers, quantum key distribution relies on the unpredictable nature of quantum mechanics, in this case to distribute unique keys between two users without any third party being able to listen in. One of the most common methods is to encode the cryptographic key into the orientation of a photon and send that photon to the other person. To achieve full security, we need to combine quantum key distribution with one-time pads to encrypt our messages, which will still require extremely fast random number generators.
We believe these quantum random number generators will be able to provide all the random numbers we’ll ever need. We’ll also have to continually check that our quantum sources are free from defect and interference and are producing numbers that are truly random. At our lab, we’ve developed a method for determining how confident we can be in a source’s true randomness. Our “randomness metrology” begins with establishing both the physical process that the source uses and the precision of the source’s measurements. We can use that information to set a boundary on how much of the randomness is arising purely from the quantum process.
Now that we’ve taken the first steps in developing quantum random number generators that are small enough, cheap enough, and fast enough for widespread, everyday use, the next step will be to install and test them in computers, smartphones, and IoT devices. With true random number generators, we can produce unpredictable cryptographic keys, and if we combine those keys with a secure method to distribute them, no longer will we have to worry about the computational or mathematical skills of an enemy—even the most capable attacker is powerless against true unpredictability. Nearly a century and a half after Frank Miller proposed his one-time pad, unbreakable security could finally be within our grasp.
This article appears in the July 2018 print issue as “The Future of Cybersecurity Is Quantum.”
About the Authors
Carlos Abellán is CEO of the quantum cryptography startup Quside, in Barcelona. Valerio Pruneri is a cofounder of Quside and the Corning Inc. chair and leader of the optoelectronics group at the Institute of Photonic Sciences, also in Barcelona.


