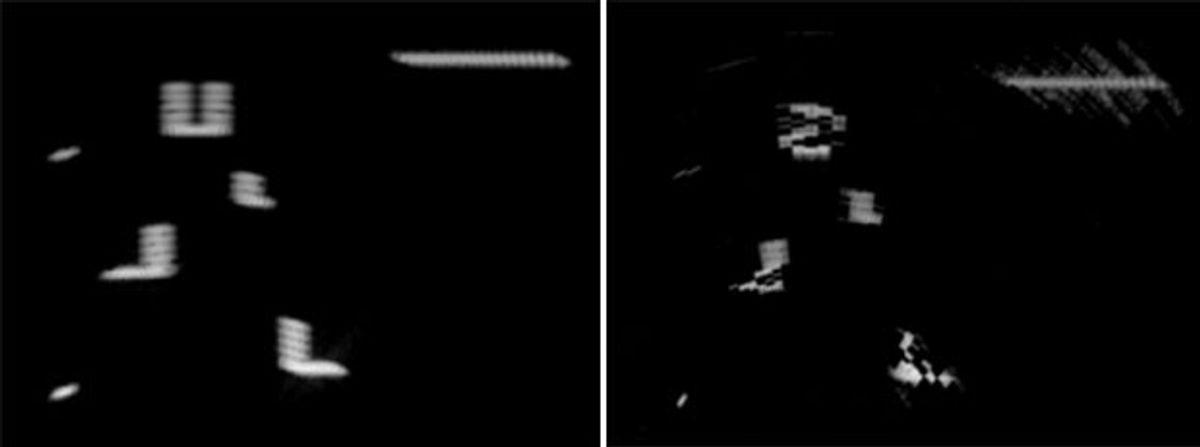
There are some stumbling block along the path to workable terahertz wave imaging. Building antenna arrays is one. Handling the information the arrays generate is another.
While some researchers have turned to metamaterials to cut down the bulk of terahertz antennas, a team at MIT is working on ways of doing more with less—fewer antennas and less computation—to smooth the road to low-cost mobile radars and sensitive detectors for explosives and firearms.
James Krieger, Yuval Kochman (now at the Hebrew University of Jerusalem), and Gregory Wornell report on strategies for faster, less expensive antenna design, signal-analysis, and error-correction in IEEE Transactions on Antennas and Propagation.
Terahertz radiation falls into the range between microwaves and visible light, at frequencies of 300 billion Hertz to 10 trillion Hz and wavelengths of 1000 to 30 micrometers. In a traditional phased array, antenna elements must be no farther than one-half a wavelength apart. A real-world application (such as an automotive collision-avoidance system that Krieger and his colleagues use as an example) might require an aperture of roughly 2 meters to properly resolve moving, vehicle-size objects. So a conventional array built to image signals at 100 GHz (with a 3 mm wavelength) would require on the order of 1000 antennas, while a 1 THz array would need about 10 000. Building such arrays is costly and complex in its own right. And the computational power needed to resolve the phased array’s signals into a 2-D image increases with the number of antennas—a demand that “quickly becomes impracticably large,” according the MIT group.
But one-antenna-every-half-wavelength resolution is only truly necessary if all objects of interest stand shoulder to shoulder at the same distance from the array. In the real world—a parking lot, say—targets are “sparse,” generally few and far between at any range or azimuth.
"Think about a range around you, like five feet," said Wornell, the team leader. "There's actually not that much at five feet around you. Or at 10 feet. Different parts of the scene are occupied at those different ranges, but at any given range, it's pretty sparse. Roughly speaking, the theory goes like this: If, say, 10 percent of the scene at a given range is occupied with objects, then you need only 10 percent of the full array to still be able to achieve full resolution."
The trick is to come up with a method for deciding which half, quarter, fifth, or tenth of the possible antenna locations to populate. The MIT group breaks the array down into number of “periods,” each with the same number of lattice points one-half wavelength apart. (Periods with prime numbers of lattice points make for the easiest calculations.) The key is to select positions so that the range of distances between pairs of antennas covers the range of possible separations as evenly as possible. This is fairly easy to calculate directly with periods of 7 or 11 lattice points; it’s trickier for periods of 37, 47, or 57 nodes, but an iterative tactic (like the Markov Chain Monte Carlo method) produces workable positioning patterns.
The periodic approach cuts down computing overhead by breaking the antennas down into “cosets” within each period. Coset data are collected, compared, and analyzed together, so the computational demand goes up with the number of antennas in a period, not with the total number of antennas.
In the 100 GHz parking lot simulation, a conventional phased array would require 987 individual antennas to attain the necessary 2-meter aperture. With the addition of algorithms for detecting and filtering out errors, the Wornell group’s multi-coset sparse array built usable images with as few as 105 antennas. (Remember, these are linear arrays producing a 2-D image. So a two-dimensional arrays to generate 3-D images would square the number of antennas needed—to about a million for a conventional array versus about 10 000 for a multi-coset sparse array.)
Douglas McCormick is a freelance science writer and recovering entrepreneur. He has been chief editor of Nature Biotechnology, Pharmaceutical Technology, and Biotechniques.