Metcalfe’s Law is Wrong
Communications networks increase in value as they add members—but by how much? The devil is in the details
In other words, once a burgeoning network—a growing community of users of an app or online game, for instance—rounds out its initial social groups and then brings in other completed social groups, not everyone is interacting with everyone else at the same sort of rate they once had in a smaller setting. And that is part of the reason why the authors have stated Metcalfe’s law doesn’t scale up as accurately as its proponents like to think.
Which still wasn’t convincing enough for the authors of a couple papers in 2013 and 2014 as well—who made their own strenuous defense of the still-popular law of networks. Odlyzko, who remains a professor of mathematics at the University of Minnesota, says that in 2006 they thought Metcalfe’s law could lead to large networks (and companies behind those large networks) being overvalued in the larger marketplace, as the Guardian noted at the time. And while there are have been many changes to the internet and society between 2006 and 2023, Odlyzko says, “That is a concern today just as much as it was two decades ago.” —IEEE Spectrum
The law is said to be true for any type of communications network, whether it involves telephones, computers, or users of the World Wide Web. While the notion of “value” is inevitably somewhat vague, the idea is that a network is more valuable the more people you can call or write to or the more Web pages you can link to.
Metcalfe’s Law attempts to quantify this increase in value. It is named for no less a luminary than Robert M. Metcalfe, the inventor of Ethernet. During the Internet boom, the law was an article of faith with entrepreneurs, venture capitalists, and engineers, because it seemed to offer a quantitative explanation for the boom’s various now-quaint mantras, like “network effects,” “first-mover advantage,” “Internet time,” and, most poignant of all, “build it and they will come.”
By seeming to assure that the value of a network would increase quadratically—proportionately to the square of the number of its participants—while costs would, at most, grow linearly, Metcalfe’s Law gave an air of credibility to the mad rush for growth and the neglect of profitability. It may seem a mundane observation today, but it was hot stuff during the Internet bubble.
Remarkably enough, though the quaint nostrums of the dot-com era are gone, Metcalfe’s Law remains, adding a touch of scientific respectability to a new wave of investment that is being contemplated, the Bubble 2.0, which appears to be inspired by the success of Google. That’s dangerous because, as we will demonstrate, the law is wrong. If there is to be a new, broadband-inspired period of telecommunications growth, it is essential that the mistakes of the 1990s not be reprised.
The law was named in 1993 by George Gilder, publisher of the influential Gilder Technology Report. Like Moore’s Law, which states that the number of transistors on a chip will double every 18 to 20 months, Metcalfe’s Law is a rough empirical description, not an immutable physical law. Gilder proclaimed the law’s importance in the development of what came to be called “the New Economy.”
Soon afterward, Reed E. Hundt, then the chairman of the U.S. Federal Communications Commission, declared that Metcalfe’s Law and Moore’s Law “give us the best foundation for understanding the Internet.” A few years later, Marc Andreessen, who created the first popular Web browser and went on to cofound Netscape, attributed the rapid development of the Web—for example, the growth in AOL’s subscriber base—to Metcalfe’s Law.
There was some validity to many of the Internet mantras of the bubble years. A few very successful dot-coms did exploit the power of the Internet to provide services that today yield great profits. But when we look beyond that handful of spectacular successes, we see that, overall, the law’s devotees didn’t fare well. For every Yahooï»’ or Google, there were dozens, even hundreds, of Pets.coms, EToys, and Excite@Homes, each dedicated to increasing its user base instead of its profits, all the while increasing expenses without revenue.
Because of the mind-set created, at least in small part, by Metcalfe’s Law, even the stocks of rock-solid companies reached absurd heights before returning to Earth. The share price of Cisco Systems Inc., San Jose, Calif., for example, fell 89 percent—a loss of over US $580 billion in the paper value of its stock—between March 2000 and October 2002. And the rapid growth of AOL, which Andreessen attributed to Metcalfe’s Law, came to a screeching halt; the company has struggled, to put it mildly, in the last few years.
Metcalfe’s Law was over a dozen years old when Gilder named it. As Metcalfe himself remembers it, in a private correspondence with one of the authors, “The original point of my law (a 35mm slide circa 1980, way before George Gilder named it...) was to establish the existence of a cost-value crossover point—critical mass—before which networks don’t pay. The trick is to get past that point, to establish critical mass.” [See “” a reproduction of Metcalfe’s historic slide.]
Metcalfe was ideally situated to watch and analyze the growth of networks and their profitability. In the 1970s, first in his Harvard Ph.D. thesis and then at the legendary Xerox Palo Alto Research Center, Metcalfe developed the Ethernet protocol, which has come to dominate telecommunications networks. In the 1980s, he went on to found the highly successful networking company 3Com Corp., in Marlborough, Mass. In 1990 he became the publisher of the trade periodical InfoWorld and an influential high-tech columnist. More recently, he has been a venture capitalist.
The foundation of his eponymous law is the observation that in a communications network with n members, each can make (n –1) connections with other participants. If all those connections are equally valuable—and this is the big “if” as far as we are concerned—the total value of the network is proportional to n (n –1), that is, roughly, n2. So if, for example, a network has 10 members, there are 90 different possible connections that one member can make to another. If the network doubles in size, to 20, the number of connections doesn’t merely double, to 180, it grows to 380—it roughly quadruples, in other words.
If Metcalfe’s mathematics were right, how can the law be wrong? Metcalfe was correct that the value of a network grows faster than its size in linear terms; the question is, how much faster? If there are n members on a network, Metcalfe said the value grows quadratically as the number of members grows.
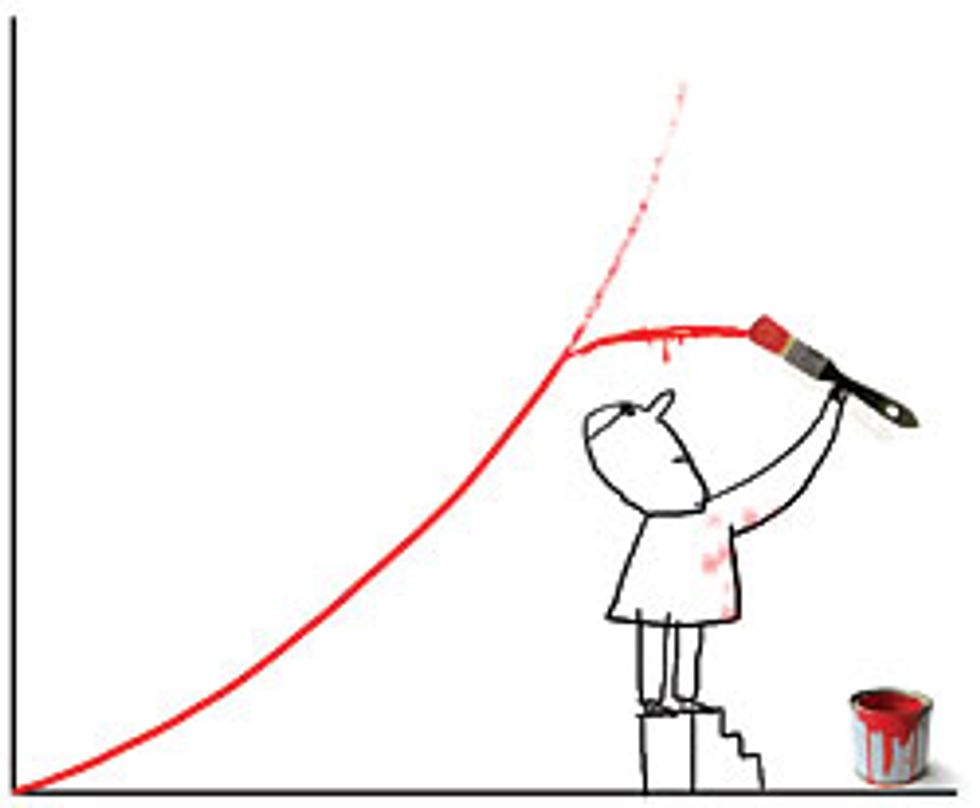
We propose, instead, that the value of a network of size n grows in proportion to n log(n). Note that these laws are growth laws, which means they cannot predict the value of a network from its size alone. But if we already know its valuation at one particular size, we can estimate its value at any future size, all other factors being equal.
The distinction between these laws might seem to be one that only a mathematician could appreciate, so let us illustrate it with a simple dollar example.
Imagine a network of 100 000 members that we know brings in $1 million. We have to know this starting point in advance—none of the laws can help here, as they tell us only about growth. So if the network doubles its membership to 200 000, Metcalfe’s Law says its value grows by (200 0002/100 0002) times, quadrupling to $4 million, whereas the n log( n ) law says its value grows by 200 000 log(200 000)/100 000 log(100 000) times to only $2.1 million. In both cases, the network’s growth in value more than doubles, still outpacing the growth in members, but the one is a much more modest growth than the other. In our view, much of the difference between the artificial values of the dot-com era and the genuine value created by the Internet can be explained by the difference between the Metcalfe-fueled optimism of n2 and the more sober reality of n log(n).
This difference will be critical as network investors and managers plan better for growth. In North America alone, telecommunications carriers are expected to invest $65 billion this year in expanding their networks, according to the analytical firm Infonetics Research Inc., in San Jose, Calif. As we will show, our rule of thumb for estimating value also has implications for companies in the important business of managing interconnections between major networks.
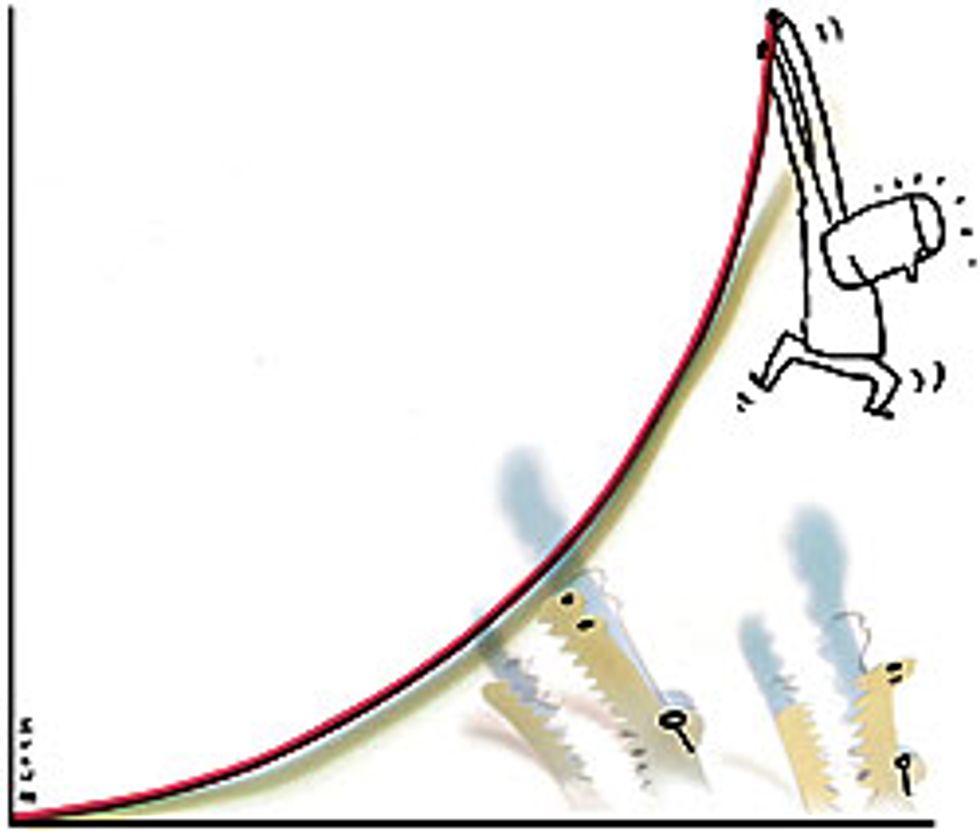
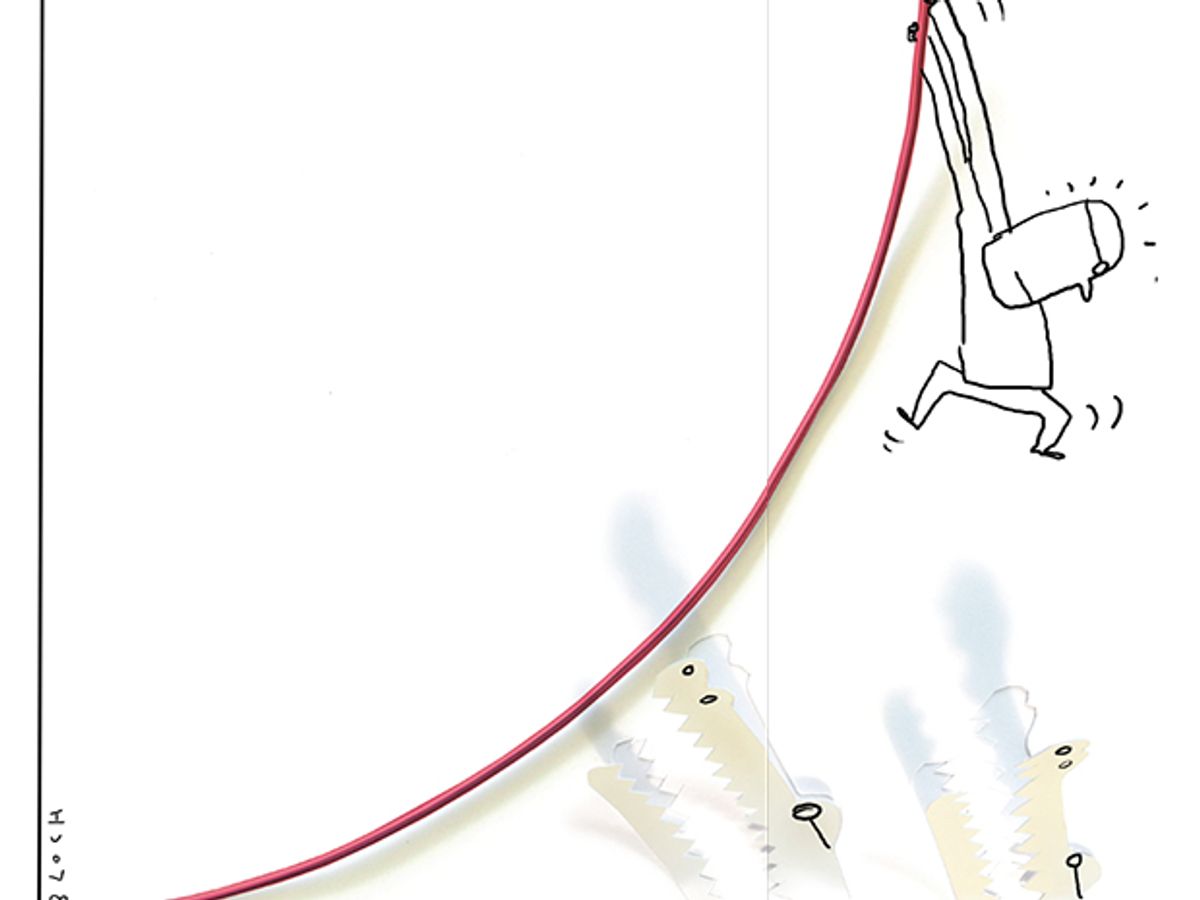
The increasing value of a network as its size increases certainly lies somewhere between linear and exponential growth [see diagram, ""]. The value of a broadcast network is believed to grow linearly; it’s a relationship called Sarnoff’s Law, named for the pioneering RCA television executive and entrepreneur David Sarnoff. At the other extreme, exponential—that is, 2n—growth, has been called Reed’s Law, in honor of computer networking and software pioneer David P. Reed. Reed proposed that the value of networks that allow the formation of groups, such as AOL’s chat rooms or Yahoo’s mailing lists, grows proportionally with 2n.
We admit that our n log(n) valuation of a communications network oversimplifies the complicated question of what creates value in a network; in particular, it doesn’t quantify the factors that subtract from the value of a growing network, such as an increase in spam e-mail. Our valuation cannot be proved, in the sense of a deductive argument from first principles. But if we search for a cogent description of a network’s value, then n log(n) appears to be the best choice. Not only is it supported by several quantitative arguments, but it fits in with observed developments in the economy. The n log(n) valuation for a network provides a rough-and-ready description of the dynamics that led to the disappointingly slow growth in the value of dot-com companies. On the other hand, because this growth is faster than the linear growth of Sarnoff’s Law, it helps explain the occasional dot-com successes we have seen.
The fundamental flaw underlying both Metcalfe’s and Reed’s laws is in the assignment of equal value to all connections or all groups. The underlying problem with this assumption was pointed out a century and a half ago by Henry David Thoreau in relation to the very first large telecommunications network, then being built in the United States. In his famous book Walden (1854), he wrote: “We are in great haste to construct a magnetic telegraph from Maine to Texas; but Maine and Texas, it may be, have nothing important to communicate.”
As it turns out, Maine did have quite a bit to communicate with Texas—but not nearly as much as with, say, Boston and New York City. In general, connections are not all used with the same intensity. In fact, in large networks, such as the Internet, with millions and millions of potential connections between individuals, most are not used at all. So assigning equal value to all of them is not justified. This is our basic objection to Metcalfe’s Law, and it’s not a new one: it has been noted by many observers, including Metcalfe himself.
There are common-sense arguments that suggest Metcalfe’s and Reed’s laws are incorrect. For example, Reed’s Law says that every new person on a network doubles its value. Adding 10 people, by this reasoning, increases its value a thousandfold (210). But that does not even remotely fit our general expectations of network values—a network with 50 010 people can’t possibly be worth a thousand times as much as a network with 50 000 people.
At some point, adding one person would theoretically increase the network value by an amount equal to the whole world economy, and adding a few more people would make us all immeasurably rich. Clearly, this hasn’t happened and is not likely to happen. So Reed’s Law cannot be correct, even though its core insight—that there is value in group formation—is true. And, to be fair, just as Metcalfe was aware of the limitations of his law, so was Reed of his law’s.
Metcalfe’s Law does not lead to conclusions as obviously counterintuitive as Reed’s Law. But it does fly in the face of a great deal of the history of telecommunications: if Metcalfe’s Law were true, it would create overwhelming incentives for all networks relying on the same technology to merge, or at least to interconnect. These incentives would make isolated networks hard to explain.
To see this, consider two networks, each with n members. By Metcalfe’s Law, each one’s value is on the order of n2, so the total value of both of these separate networks is roughly 2n2. But suppose these two networks merge. Then we will effectively have a single network with 2n members, which, by Metcalfe’s Law, will be worth (2n)2 or 4n2—twice as much as the combined value of the two separate networks.
Surely it would require a singularly obtuse management, to say nothing of stunningly inefficient financial markets, to fail to seize this obvious opportunity to double total network value by simply combining the two. Yet historically there have been many cases of networks that resisted interconnection for a long time. For example, a century ago in the United States, the Bell System and the independent phone companies often competed in the same neighborhood, with subscribers to one being unable to call subscribers to the other. Eventually, through a combination of financial maneuvers and political pressure, such systems connected with one another, but it took two decades.
Similarly, in the late 1980s and early 1990s, the commercial online companies such as CompuServe, Prodigy, AOL, and MCIMail provided e-mail to subscribers, but only within their own systems, and it wasn’t until the mid-1990s that full interconnection was achieved. More recently we have had (and continue to have) controversies about interconnection of instant messaging systems and about the free exchange of traffic between Internet service providers. The behavior of network operators in these examples is hard to explain if the value of a network grows as fast as Metcalfe’s n2.
There is a further argument to make about interconnecting networks. If Metcalfe’s Law were true, then two networks ought to interconnect regardless of their relative sizes. But in the real world of business and networks, only companies of roughly equal size are ever eager to interconnect. In most cases, the larger network believes it is helping the smaller one far more than it itself is being helped. Typically in such cases, the larger network demands some additional compensation before interconnecting. Our n log(n) assessment of value is consistent with this real-world behavior of networking companies; Metcalfe’s n2 is not. [See sidebar, "Making the Connection" for the mathematics behind this argument.]
We have, as well, developed several quantitative justifications for our n log(n) rule-of-thumb valuation of a general communications network of size n . The most intuitive one is based on yet another rule of thumb, Zipf’s Law, named for the 20th-century linguist George Kingsley Zipf.
Zipf’s Law is one of those empirical rules that characterize a surprising range of real-world phenomena remarkably well. It says that if we order some large collection by size or popularity, the second element in the collection will be about half the measure of the first one, the third one will be about one-third the measure of the first one, and so on. In general, in other words, the k th-ranked item will measure about 1/ k of the first one.
To take one example, in a typical large body of English-language text, the most popular word, “the,” usually accounts for nearly 7 percent of all word occurrences. The second-place word, “of,” makes up 3.5 percent of such occurrences, and the third-place word, “and,” accounts for 2.8 percent. In other words, the sequence of percentages (7.0, 3.5, 2.8, and so on) corresponds closely with the 1/ k sequence (1/1, 1/2, 1/3…). Although Zipf originally formulated his law to apply just to this phenomenon of word frequencies, scientists find that it describes a surprisingly wide range of statistical distributions, such as individual wealth and income, populations of cities, and even the readership of blogs.
To understand how Zipf’s Law leads to our n log( n ) law, consider the relative value of a network near and dear to you—the members of your e-mail list. Obeying, as they usually do, Zipf’s Law, the members of such networks can be ranked in the same sort of way that Zipf ranked words—by the number of e-mail messages that are in your in-box. Each person’s e-mails will contribute 1/ k to the total “value” of your in-box, where k is the person’s rank.
The person ranked No. 1 in volume of correspondence with you thus has a value arbitrarily set to 1/1, or 1. (This person corresponds to the word “the” in the linguistic example.) The person ranked No. 2 will be assumed to contribute half as much, or 1/2. And the person ranked k th will, by Zipf’s Law, add about 1/ k to the total value you assign to this network of correspondents.
That total value to you will be the sum of the decreasing 1/ k values of all the other members of the network. So if your network has n members, this value will be proportional to 1 + 1/2 + 1/3 +… + 1/( n –1), which approaches log( n ). More precisely, it will almost equal the sum of log( n ) plus a constant value. Of course, there are n -1 other members who derive similar value from the network, so the value to all n of you increases as n log( n ).
Zipf’s Law can also describe in quantitative terms a currently popular thesis called The Long Tail. Consider the items in a collection, such as the books for sale at Amazon, ranked by popularity. A popularity graph would slope downward, with the few dozen most popular books in the upper left-hand corner. The graph would trail off to the lower right, and the long tail would list the hundreds of thousands of books that sell only one or two copies each year. The long tail of the English language—the original application of Zipf’s Law—would be the several hundred thousand words that you hardly ever encounter, such as “floriferous” or “refulgent.”
Taking popularity as a rough measure of value (at least to booksellers like Amazon), then the value of each individual item is given by Zipf’s Law. That is, if we have a million items, then the most popular 100 will contribute a third of the total value, the next 10 000 another third, and the remaining 989 900 the final third. The value of the collection of n items is proportional to log(n).
Incidentally, this mathematics indicates why online stores are the only place to shop if your tastes in books, music, and movies are esoteric. Let’s say an online music store like Rhapsody or iTunes carries 735 000 titles, while a traditional brick-and-mortar store will carry 10 000 to 20 000. The law of long tails says that two-thirds of the online store’s revenue will come from just the titles that its physical rival carries. In other words, a very respectable chunk of revenue—a third—will come from the 720 000 or so titles that hardly anyone ever buys. And, unlike the cost to a brick-and-mortar store, the cost to an online store of holding all that inventory is minimal. So it makes good sense for them to stock all those incredibly slow-selling titles.
At a time when telecommunications is the key infrastructure for the global economy, providers need to make fundamental decisions about whether they will be pure providers of connectivity or make their money by selling or reselling content, such as television and movies. It is essential that they value their enterprises correctly—neither overvaluing the business of providing content nor overvaluing, as Metcalfe’s Law does, the business of providing connectivity. Their futures are filled with risks and opportunities. We believe if they value the growth in their networks as n log( n ), they will be better equipped to navigate the choppy waters that lie ahead.
About the Authors
BOB BRISCOE is chief researcher at Networks Research Centre, BT (formerly British Telecom), in Ipswich, England.
ANDREW ODLYZKO is a professor of mathematics and the director of the Digital Technology Center at the University of Minnesota, in Minneapolis.
BENJAMIN TILLY is a senior programmer at Rent.com, a dot-com company that actually made money, in Santa Monica, Calif.
To Probe Further
David P. Reed argues for his law in “The Sneaky Exponential” on his Web site at https://www.reed.com/Papers/GFN/reedslaw.html.
Several additional quantitative arguments are made for the n log(n) value for Metcalfe’s Law on the authors’ Web sites at https://www.cs.ucl.ac.uk/staff/B.Briscoeand https://www.dtc.umn.edu/~odlyzko.
Chris Anderson’s article “The Long Tail” was featured in the October 2004 issue of Wired. Anderson now has an entire Web site devoted to the topic at https://www.thelongtail.com.
George Gilder dubbed Metcalfe’s observation a law in his “Metcalfe’s Law and Legacy,” an article that was published in the 13 September 1993 issue of Forbes ASAP.
An article in the December 2003 issue of IEEE Spectrum, “5 Commandments,” which can be found at /dec03/5com, discusses Moore’s and Metcalfe’s laws, as well as three others: Rock’s Law (“the cost of semiconductor tools doubles every four years”); Machrone’s Law (“the PC you want to buy will always be $5000”); and Wirth’s Law (“software is slowing faster than hardware is accelerating”).