Making Unbreakable Code
The quantum properties of photons could make encrypted messages absolutely secure
The battle between code-makers and code-breakers is centuries old, but at the start of the 21st century, could it finally be drawing to a close? Physicists are putting the finishing touches on a method of encrypting messages that is more secure than anything that has gone before. Unlike the ciphers of the past, this new method has the potential to be absolutely unbreakable--not just practically unbreakable, as the makers of the World War II Enigma machines thought and the users of today's public key encryption hope, but theoretically unbreakable. Mathematicians believe they can prove it.
Central to the technique are the strange laws of quantum mechanics that govern the universe on the smallest scale, and the ability to exploit physics on this scale has generated huge interest. Already experimental messages encrypted using quantum mechanics are being sent over tens of kilometers of optical fibers and received securely. Last summer the first portable quantum cryptography machine was unveiled at the Los Alamos National Laboratory in New Mexico. Richard Hughes, the Los Alamos researcher who led the machine's development, says it can send encrypted messages through the air over dozens of kilometers and works day or night in good weather and in bad. And in Geneva, Switzerland, a small start-up, ID Quantique, has begun marketing a quantum cryptography machine.
Indeed, researchers are confident that it will not be long before ultra-secret messages are routinely transmitted in this way. "We hope to have the first commercial system working later this year," says Gregoire Ribordy, the physicist who runs ID Quantique. If that happens, the implications for secure communications could be profound.
But while quantum cryptography may be perfect in theory, practical considerations introduce security loopholes that an eavesdropper can exploit. The seriousness of these is still unclear, and physicists believe they can plug most of the holes with more efficient equipment. Still, enough cracks remain to maintain a healthy interest among cryptographers.
An old idea made new
Quantum cryptography's power comes from its ability to exploit a method of encryption known as the one-time pad. The method was invented toward the end of World War I when a group of engineers at the American Telephone and Telegraph Co. took on the seemingly impossible task of securing the nation's burgeoning web of telegraph wires, then clearly vulnerable to eavesdroppers.
It had been common practice for centuries to encrypt a message by altering it in some reversible way. Cryptographers often begin by converting each letter in the message to its ordinal position in the alphabet. An F, for example, becomes 7, and a W becomes 23. The message is then altered by, for instance, adding two to each number, moving each letter two places up the alphabet, with Y becoming A and Z becoming B.
This technique creates a ciphertext that is unintelligible to the casual reader but easily decodable by anyone who knows the trick. The ciphertext can be made more difficult to crack by converting another piece of text such as a verse from Shakespeare into numeric form and then adding it letter by letter to the secret message. This added text is known as a key. If the receiver knows the key, he or she can easily decode the message by subtracting the key from the ciphertext.
In tackling the telegraphy problem, Gilbert Vernam at AT&T and Major Joseph O. Mauborgne, head of cryptographic research for the U.S. Army Signal Corps, hit upon a new kind of cipher. Vernam suggested using a key consisting of random letters, which become random numbers. If the key were random, that is, if the sequence of numbers in the key had no pattern or structure of any kind, the ciphertext would be random, too. Without any pattern to latch on to--such as the prevalence of the letter "e" in English texts--an eavesdropper is powerless to decipher the message. Mathematicians have since proven as much.
By using a new, randomly generated key for each message, Mauborgne realized that he could guarantee secrecy every time. What the two cryptographers had discovered was the so-called one-time pad, the only form of encryption known that has been proven to be secure.
(The term alludes to the practice of using a pad of hundreds of sheets of paper, with each sheet containing lines of a unique and random sequence of letters. The sender has one pad; the person who is to receive a message has a copy of it. For each communication, one sheet is used to encode the message, the corresponding sheet, to decode it. After the message is deciphered, both sheets are destroyed, hence the name one-time pad.)
But the battle between code-makers and code-breakers was by no means over. The one-time pad has its own peculiar weaknesses. For a start, the key must be at least as long as the message it is intended to encrypt, making it cumbersome to use. More importantly, a copy of the key must somehow be distributed to the message's intended receiver, no easy task because doing this securely presents huge logistical problems, particularly for communications networks where several users need to communicate with each other in private. Indeed, the practical problems with one-time pads are so great that they are used only when the greatest privacy is required--like for the hotline between political leaders in Washington and Moscow.
Of course, encryption of transmitted data is just one part of keeping information secret. In fact, decoding intercepted transmissions these days is rare, because cracking even average consumer encryption is so hard. It is far easier for a would-be interceptor to compromise other aspects of the overall process that are much more vulnerable than encryption, like hacking the sender's hard drive before the data is encrypted for transmission.
Still, technologies such as quantum cryptography are being developed today with an eye toward a future in which code-cracking might become practical. Though they are far from powerful enough now, a quantum computer may one day be able to crack today's codes. A one-time pad, however, remains unassailable even by those future technologies, and that is where quantum cryptography fits in.
The genius of quantum cryptography is that it solves the problem of key distribution. This ability comes directly from the way quantum particles such as photons behave in nature and the fact that the information these particles carry can take on this behavior. Sending a message using photons is straightforward since one of their quantum properties, polarization, can be used to represent a 0 or a 1. Each photon therefore carries one bit of quantum information, which physicists call a qubit.
To receive such a qubit, the recipient must determine the photon's polarization, a measurement that inevitably alters the photon's properties. This is bad news for eavesdroppers since the sender and receiver can easily spot the alterations these measurements cause. Of course, cryptographers cannot exploit this idea to send private messages since the security can only be determined in retrospect.
Instead they send a series of photons with random polarizations. This sequence can then be used to generate a sequence of numbers that is analogous to the letters on the one-time pad that Mauborgne used. The process is known as quantum key distribution. If the key is intercepted, no matter, it is only a set of random bits and can be discarded. The sender can then transmit another key. Once a key has been securely received, it can be used as a one-time pad to encrypt a message that can then be transmitted by conventional means--telephone, e-mail, or carrier pigeon.
A practical plan
In 1984 Charles H. Bennett at IBM Laboratories (now the Thomas J. Watson Research Center, Yorktown Heights, N.Y.) and Gilles Brassard at the University of Montreal devised the first workable quantum cryptography scheme, which has consequently become known as the BB84 protocol.
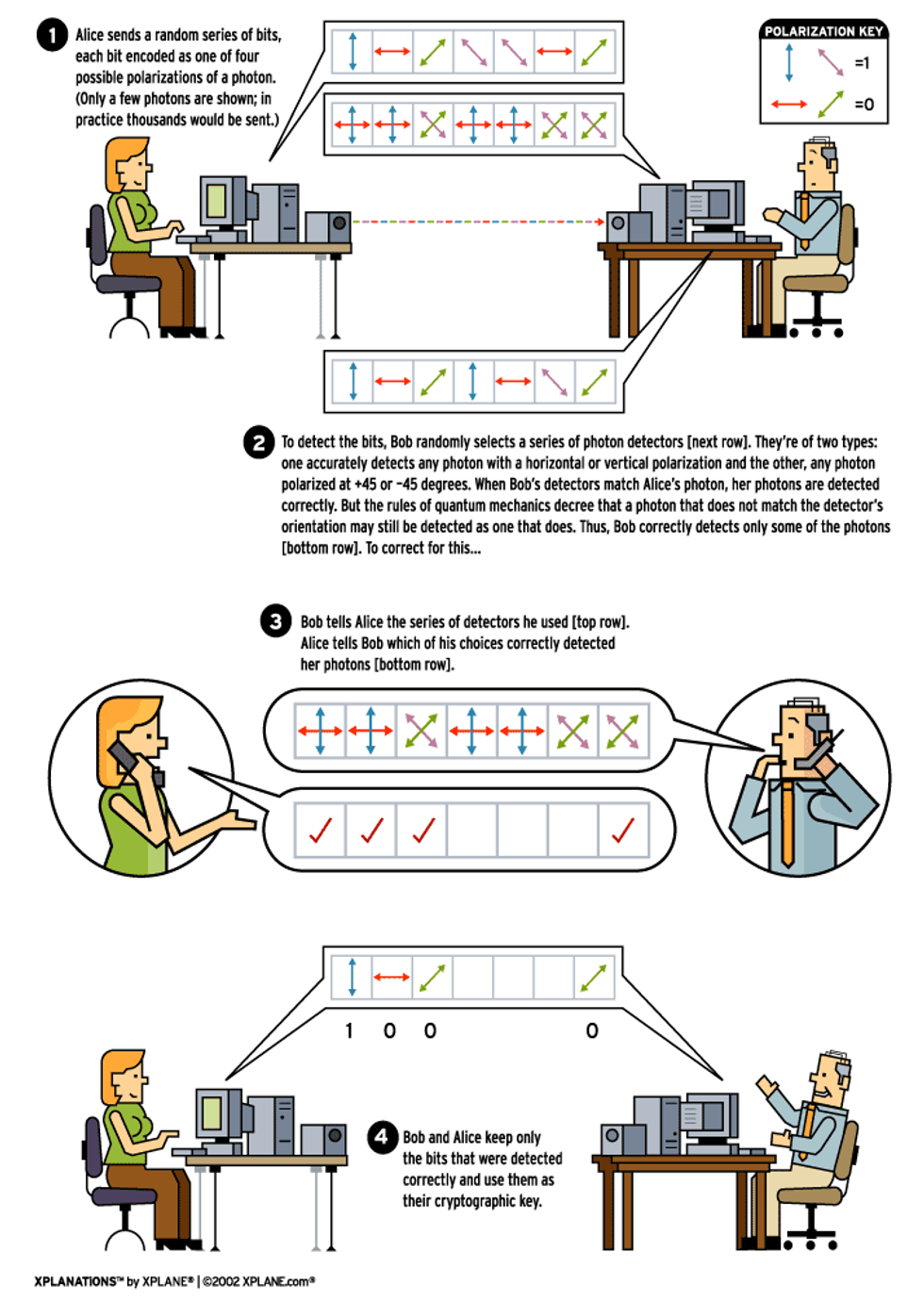
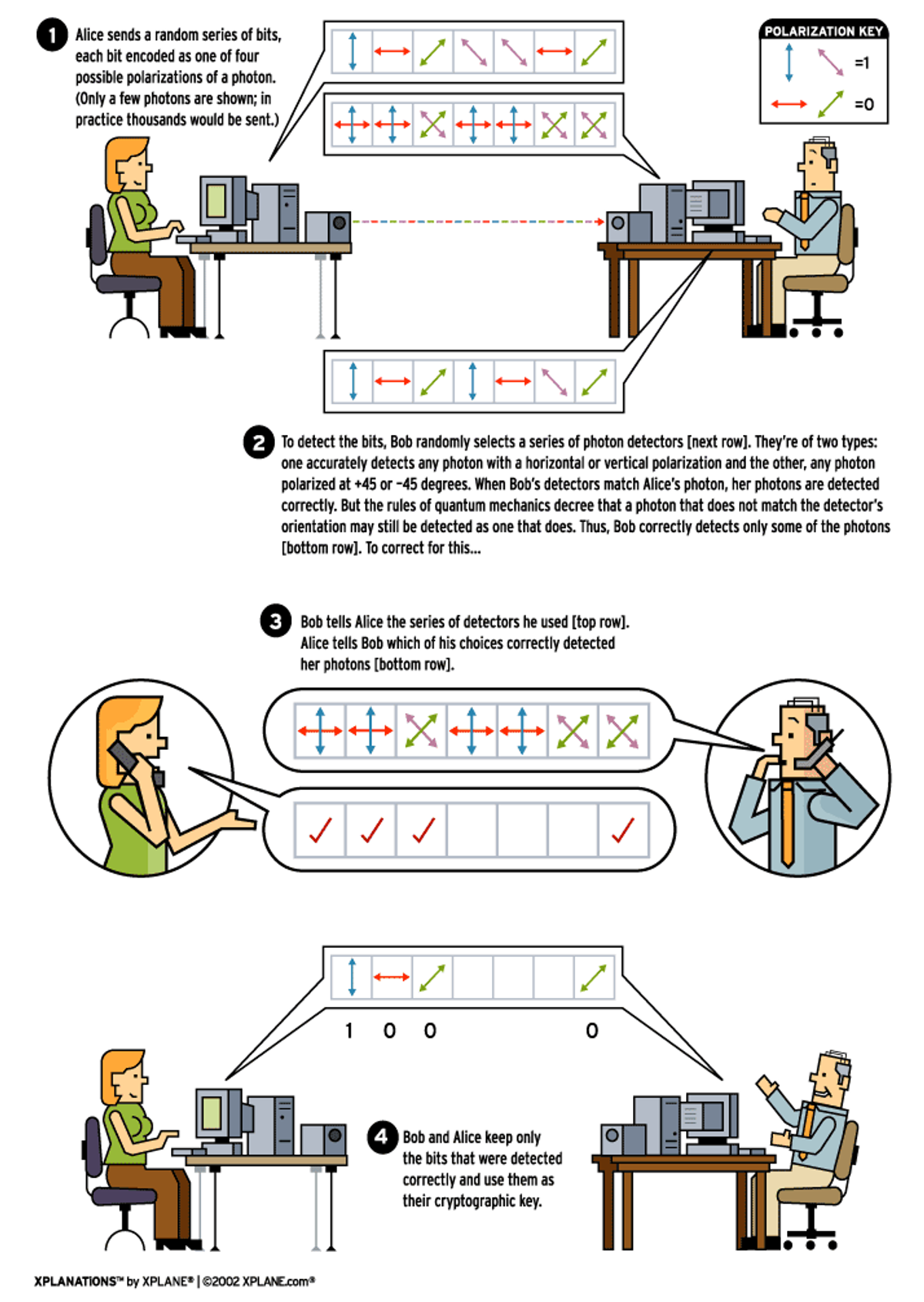
In the protocol, the sender, Alice, is trying to transmit a secure message to the receiver, Bob. Alice begins by sending Bob a random series of qubits [see illustration, above]. Since Alice is using photons to transmit her qubits, she can encode them on the following so-called rectilinear basis: a vertical polarization represents a 1 and a horizontal polarization represents a 0. Alice can also use photons on a diagonal basis so that a +45 degree orientation represents a 1 and -45 degrees represents a 0. The fact that she has two bases to choose from turns out to be important.
To receive Alice's qubits, Bob uses a polarization beam-splitter, a device that shunts photons of one polarization to one side while allowing photons of an orthogonal polarization to pass through. With the device, Bob can correctly measure only photons of a specific basis. For example, in the rectilinear basis, he can properly measure photons from Alice with a vertical or horizontal polarization, but not diagonally polarized photons.
Because of their quantum nature, diagonally polarized photons encountering a rectilinear beam-splitter appear to Bob to have either a vertical or a horizontal polarization, with equal probability. This same phenomenon holds true for rectilinear-basis photons encountering a diagonal beam splitter. Part of the utility of BB84 is that it offers Bob a way to discard these incorrect measurements.
Alice can use either basis to encode each qubit, but the important requirement is that she makes her choice at random. Similarly, Bob measures each of the incoming photons, choosing at random either basis. Clearly, whenever they use the same basis, they get the same results, and whenever they use opposite bases, the results may not match up.
Bob then publicly--that is, with no need for secrecy or encryption--announces the series of choices he made: rectilinear, rectilinear, diagonal, rectilinear, diagonal, rectilinear, rectilinear, and so on. But he does not reveal the results of his measurements. Alice then tells Bob publicly which of his choices of base match hers. They then keep only the results from the measurements made when the bases happened to match and discard the rest. That's how Bob is able to ignore the photons measured in the wrong basis.
What they are left with is a shorter series of random bits known only to Alice and Bob that they can use as a one-time pad in the conventional way. Note that neither Alice nor Bob can determine the key in advance. Instead it is the result of both their random choices.
In the real world, one more step remains. Photons can become accidentally altered on their way from Bob to Alice, and detection equipment is not perfect. So Bob and Alice will not have perfectly matching keys. To weed out the bad bits, they must perform some standard error correction schemes.
One is for each to divide his or her key into blocks of perhaps tens of sequential bits and compute the parity for each block. That is, they determine if the number of 1s in the block is odd or even. They then compare the parity values. If Bob and Alice get the same value for a block, they assume there are no errors in that block. But if the parity differs for a particular block, they must further divide that block and compute and compare the parities, progressively homing in on the errant bit or bits.
To keep from revealing too much information about the key when they go through the process, Bob and Alice throw out one bit for each time they compare a parity value. This process must be repeated many times, using different ways to divide up the key, and it is often also followed by other error correction algorithms. But the end result is a perfect, if shorter, key shared between them.
Incidentally, BB84 is by no means the only protocol for quantum cryptography. In 1991, Artur Ekert, a physics professor at the University of Oxford (UK), developed a scheme in which Alice and Bob use entangled photons to distribute a key. Entangled photons are particles linked by a phenomenon of quantum mechanics in such a fundamental way that a measurement on one instantly influences the state of the other, no matter how far apart they may be.
For instance, photons can be entangled so that if one is measured to have a polarization of +45 degrees, the other's polarization must be -45 degrees. Alice and Bob distribute the key by performing measurements on their half of a stream of entangled pairs and then announcing their choices of bases publicly, as they do in the BB84 protocol. The result is a shared, secret random key they can use as a one-time pad. Other schemes exist that exploit as few as two quantum states and as many as six states, as opposed to the four in BB84.
Eavesdropping attempts
Now imagine the attempts of an eavesdropper, Eve, to listen in to the key as it is being determined using BB84. She has a variety of ways of doing this, none successful. She could, for instance, intercept a photon so that it doesn't reach Bob. But then he will simply tell Alice that he never received it and they can discard that bit.
Another eavesdropping strategy is for Eve to intercept and read each photon and resend it to Bob. But this scheme also fails, according to work done in 1982 by William Wootters at Williams College (Williamstown, Mass.) and Wojciech Zurek, now at Los Alamos National Laboratory. The two showed that copying an unknown quantum state is impossible.
After all, how would Eve do it? She has no way of knowing the basis that Alice used to polarize each photon. She can guess, of course, but any wrong guesses would introduce errors or noise into Bob's data, which he will eventually notice when he and Alice try to settle on a code [see illustration].
Even if Eve guesses right, measuring, say, a vertical photon, she cannot be sure she was correct. Because of the photon's quantum nature, there is a 50 percent chance that a photon with ± 45 degree orientation could have appeared at the vertical detector. So she has no way of knowing for certain the original polarization. The inability to copy an unknown quantum state is a key difference between ordinary and quantum information and explains why quantum information is so attractive to cryptographers.
The errors Eve introduces also give her away. To determine if Eve has been listening in, Bob and Alice sacrifice a portion of their key, by publicly revealing the measured values of a small number of bits. If in comparing this portion of their key, they discover more errors than they would otherwise have expected from imperfections in their equipment, they know Eve has been intercepting their photons. For this reason, accurately measuring the error rate is important in quantum cryptography because it is Alice and Bob's way of spotting eavesdroppers.
Nevertheless, Eve can make herself difficult to find. She may decide to measure only a small fraction of the photons and thereby increase the error rate only marginally, something that in practice would be very hard for Alice and Bob to notice. Although such a tiny interception reduces Eve's potential knowledge of the key, she may be able to use whatever snippets she has.
But there is a way for Alice and Bob to minimize the information Eve can get by using so-called privacy amplification protocols. In one such algorithm, Alice, at random, picks pairs of bits from the key and performs an exclusive OR (XOR) logic operation on them, which finds their sum modulo 2 (so 0 + 0 = 0, 1+ 0 = 1, and 1 + 1 = 0). She tells Bob which bits she did the operation on, but does not share the result. He then carries out the same operation, getting the same result.
Bob and Alice next replace each pair with the calculated XOR value. Meanwhile, if Eve, who has many errors in her key, tries the same operation, it only compounds her mistakes. For example, if she knows one bit of a pair for certain but not the other, she cannot correctly compute the XOR value that Alice and Bob will use to replace the one bit Eve actually had right. Generally, as long as Bob has more information about the key than Eve, Bob and Alice can "amplify" their privacy like this.
While quantum cryptography is provably secure in eavesdropping situations like these, physicists have yet to complete the mathematical proofs that guarantee its security against all the eavesdropping strategies at Eve's disposal. In particular, physicists know that if Alice and Bob have perfect equipment, the secrecy of their messages can be guaranteed. But they also know that loopholes exist when the equipment isn't perfect, as is inevitable in real life. Just how serious these loopholes are remains to be seen.
Wanted: one photon gun
Essentially two technologies make quantum key distribution possible: the equipment for creating single photons and that for detecting them. The ideal source is a so-called photon gun that fires a single photon on demand. As yet, nobody has succeeded in building a practical photon gun, but several research efforts are under way.
Jungsang Kim at Stanford University (California) and colleagues, for example, are working on a light-emitting p-n junction that produces well-spaced single photons on demand. Others are working with a diamond-like material in which one carbon atom in the structure has been replaced with nitrogen. That substitution creates a vacancy similar to a hole in a p-type semiconductor, which emits single photons when excited by a laser. Many groups are also working on ways of making single ions emit single photons.
None of these technologies, however, is mature enough to be used in current quantum cryptography experiments. As a result, physicists have to rely on other techniques that are by no means perfect from a security viewpoint.
Most common is the practice of reducing the intensity of a pulsed laser beam to such a level that, on average, each pulse contains only a single photon. The problem here is the small but significant probability that the pulse contains more than one photon. This extra photon is manna for Eve, who can exploit the information it contains without Alice and Bob being any the wiser.
Single-photon detection is tricky too. The most common method exploits avalanche photodiodes. These devices operate beyond the diode's breakdown voltage, in what is called Geiger mode. At that point, the energy from a single absorbed photon is enough to cause an electron avalanche, an easily detectable flood of current. But these devices are far from perfect. To detect another photon, the current through the diode must be quenched and the device reset, a time-consuming process.
Furthermore, silicon's best detection wavelength is 800 nm, and it is not sensitive to wavelengths above 1100 nm, well short of the 1300 nm and 1550 nm standards for telecommunication. At telecommunications wavelengths, germanium or indium-gallium-arsenide detectors must be used, even though they are far less efficient and must be cooled well below room temperature. While commercial single-photon detectors at telecommunications wavelengths are beginning to appear on the market, they still lack the efficiencies useful for quantum cryptography.
Long-distance calls
Despite the limitations of the equipment available, researchers have made great strides in actually carrying out quantum cryptography. The first demonstration took place in the early 1990s when Charles Bennett and his colleagues at IBM carried out experiments sending photons over a distance of 30 cm through air. Improvements have been made since then. In January 2001, John Rarity and his colleagues at the UK's Defense Evaluation and Research Agency (Malvern) announced they had used the technique to communicate securely through the atmosphere over a distance of 2 km.
In New Mexico, Richard Hughes and his collaborators at Los Alamos National Laboratory are currently testing a portable system that can fit in the back of a small trailer and works, on a clear night, over 45 km. The Los Alamos group has other ambitious plans. Its portable device is the precursor of a system that could, on a clear night, beam single photons to orbiting satellites, thereby securing their transmissions. Hughes has even proposed a way for Bob and Alice to exchange a key by a satellite hookup and is currently designing a satellite-to-ground experiment to test it. "We're looking at a possible launch in four or five years," he says.
Where progress has been greatest and where most experimental work has been focused, however, is on optical-fiber-based communications, because of its ability to carry photons farther with greater reliability. At the University of Geneva (Switzerland), Nicolas Gisin and colleagues have employed the BB84 protocol to send messages over a distance of more than 60 km, using commercial optical fibers at a wavelength of 1300 nm. It is this work that Grégoire Ribordy at ID Quantique hopes to commercialize. Los Alamos National Laboratory has a similar system, which its researchers say could be used to guarantee the security of communications over public networks, between government agencies in Washington, D.C., for example.
The limitation is, of course, that optical fiber can carry a signal only so far before that signal needs a boost. Conventionally, that boost is given by optical repeaters, optoelectronic devices that absorb, amplify, and retransmit the signal. But that process would necessarily alter the quantum information a photon carries, making quantum key distribution impossible. For that reason, Alice and Bob must be linked directly by their own length of optical fiber, one that does not house any repeaters.
While quantum cryptography tempts code-makers with the promise of perfect security, in practice enough loopholes and limitations still exist to keep code-breakers busy for some time to come. So the age-old battle for totally secure communications is far from over.
Samuel K. Moore, Editor
About the Author
JUSTIN MULLINS writes about science as a freelancer based in Oxford, England. He is a consulting technology editor for New Scientist.
To Probe Further
Two articles by Michael A. Caloyannides in previous issues of IEEE Spectrum should help situate quantum cryptography in the universe of privacy: "Encryption wars: early battles," April 2000, Vol. 37, pp. 37-43, and "Encryption wars: shifting tactics," May 2000, Vol. 37, pp. 46-51.
The Code Book by Simon Singh (Doubleday, New York, 1999) is a readable romp through the history of cryptography, including present-day quantum cryptography efforts.
For a thorough review that assumes an understanding of quantum mechanics, check out "Quantum Cryptography," by Nicolas Gisin and others, at https://xxx.lanl.gov/abs/quant-ph/0101098.
Richard Hughes and colleagues presented their quantum-cryptography-for-satellites scheme in the Proceedings of the 2000 IEEE Aerospace Conference, Vol. 1, pp. 191-200.