Introducing the World’s Most Precise Clock
An optical-lattice clock could lose just a second every 13.8 billion years

In 1967, time underwent a dramatic shift. That was the year the key increment of time—the second—went from being defined as a tiny fraction of a year to something much more stable and fundamental: the time it takes for radiation absorbed and emitted by a cesium atom to undergo a certain number of cycles.
This change, which was officially adopted in the International System of Units, was driven by a technological leap. From the 1910s until the mid-1950s, the most precise way of keeping time was to synchronize the best quartz clocks to Earth’s motion around the sun. This was done by using telescopes and other instruments to periodically measure the movement of stars across the sky. But in 1955, the accuracy of this method was easily bested by the first cesium atomic clock, which made its debut at the United Kingdom’s National Physical Laboratory, on the outskirts of London.
Cesium clocks, which are essentially very precise oscillators, use microwave radiation to excite electrons and get a fix on a frequency that’s intrinsic to the cesium atom. When the technology first emerged, researchers could finally resolve a known imperfection in their previous time standard: the slight, irregular speedups and slowdowns in Earth’s rotation. Now, cesium clocks are so ubiquitous that we tend to forget how integral they are to modern life: We wouldn’t have the Global Positioning System without them. They also help synchronize Internet and cellphone communications, tie together telescope arrays, and test fundamental physics. Through our cellphones, or via low-frequency radio synchronization, cesium time standards trickle down to many of the clocks we use daily.

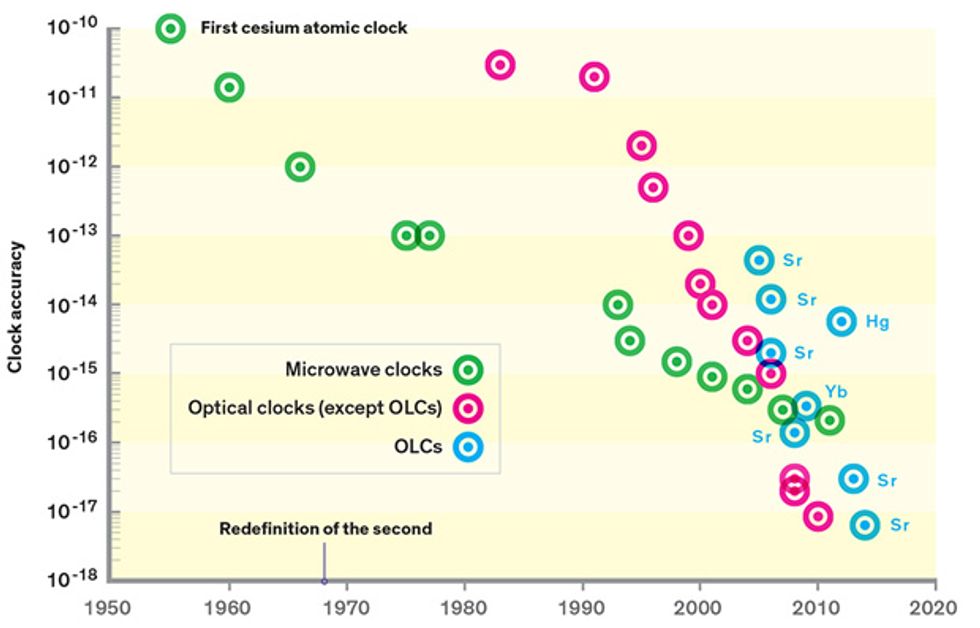
The accuracy of the cesium clock has improved greatly since 1955, increasing by a factor of 10 or so every decade. Nowadays, timekeeping based on cesium clocks accrues errors at a rate of just 0.02 nanosecond per day. If we had started such a clock when Earth began, about 4.5 billion years ago, it would be off by only about 30 seconds today.
But we can do better. A new generation of atomic clocks that use laser light instead of microwave radiation can divide time more finely. About six years ago, researchers completed single-ion versions of these optical clocks, made with an ion of either aluminum or mercury. These surpassed the accuracy of cesium clocks by a full order of magnitude.
Now, a new offshoot of this technology, the optical-lattice clock (OLC), has taken the lead. Unlike single-ion clocks, which yield one measurement of frequency at a time, OLCs can simultaneously measure thousands of atoms held in place by a powerful standing laser beam, driving down statistical uncertainty. In the past year, these clocks have managed to surpass the best single-ion optical clocks in both accuracy and stability. With further development, they will lose no more than a second over 13.8 billion years—the present-day age of the universe.
So why should you care about clocks of such mind-boggling accuracy? They are already making an impact. Some scientists are using optical-lattice clocks as tools to test fundamental physics. And others are looking at the possibility of using them to better measure differences in how fast time elapses at various points on Earth—a result of gravity’s distortion of the passage of time as described by Einstein’s theory of general relativity. The power to measure such minuscule perturbations may seem hopelessly esoteric. But it could have important real-world applications. We could, for example, improve our ability to forecast volcanic eruptions and earthquakes and more reliably detect oil and gas underground. And one day, in the not-too-distant future, OLCs could enable yet another shift in the way we define time.
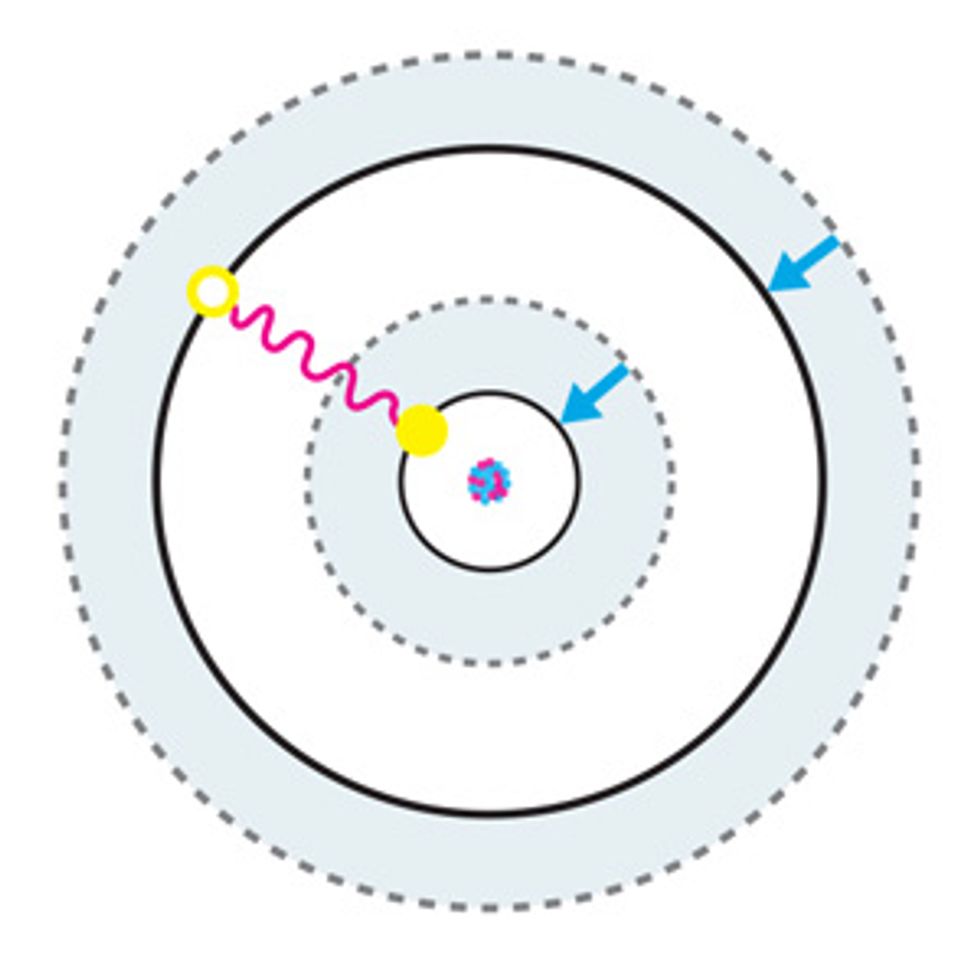
According to the rules of quantum mechanics, the energy of an electron bound to an atom is quantized. This means that an electron can occupy only one of a discrete number of orbiting zones, or orbitals, around an atom’s nucleus, although it can jump from one orbital to another by absorbing or emitting energy in the form of electromagnetic radiation. Because energy is conserved, this absorption or emission will happen only if the energy corresponding to the frequency of this radiation matches the energy difference between the two orbitals involved in the transition.
Atomic clocks work by exploiting this behavior. Atoms—of cesium, for example—are manipulated so that their electrons all occupy the lowest-energy orbital. The atoms are then hit with a specific frequency of electromagnetic radiation, which can cause an electron to jump up to a higher-energy orbital—the excited “clock state.” The likelihood of this transition depends on the frequency of the radiation that’s directed at the atom: The closer it is to the actual frequency of the clock transition, the higher the probability that the transition will occur.
To probe how often it happens, scientists use a second source of radiation to excite electrons that remain in the lowest-energy state into a short-lived, higher-energy state. These electrons release photons each time they relax back down from this transient state, and the resulting radiation can be picked up with a photosensor, such as a camera or a photomultiplier tube.
If few photons are detected, it means that electrons are largely making the clock transition, and the incoming frequency is a good match. If many photons are being released, it means that most electrons were not excited by the clock signal. A servo-driven feedback loop is used to tune the radiation source so its frequency is always close to the atomic transition.
Converting this frequency reference into a clock that ticks off the seconds requires additional steps. Generally, the frequency measured in an atomic clock is used to calibrate other frequency sources, such as hydrogen masers and quartz clocks. A “counter,” made using basic analog circuitry, can be connected to a hydrogen maser to convert its electromagnetic signal into a clock that can count off ticks to mark the time.
The most common atomic clocks today use atoms of cesium-133, which has an electron transition that lies in the microwave range of the electromagnetic spectrum. If the atom is held at absolute zero and is unperturbed (more on that in a moment), this transition will occur at a frequency of exactly 9,192,631,770 hertz. And indeed, this is how we define the second in the International System of Units—it is the time it takes for 9,192,631,770 cycles of 9,192,631,770-Hz radiation to occur.
In actuality, cesium-133 isn’t so perfect a pendulum. Atoms experience various forms of perturbation because of their imperfect environment. For example, an atom’s motion through space, which in the laboratory can easily be as fast as 100 meters per second, can shift the frequency of an electron transition by means of the Doppler effect. This is the same phenomenon that affects the pitch of ambulance sirens and other sounds as the source of the sound moves relative to the listener. Interactions with the electron clouds of other atoms can also alter the energies of electron states, as can stray external electromagnetic fields.
Perturbations decrease a clock’s accuracy: how much the atom’s average frequency is shifted from its natural unperturbed value. A number of these offsets can be accounted for, and changes in clock design have helped minimize these shifts. Indeed, one of the most dramatic such improvements occurred in the early 1990s, when physicists developed the fountain clock. This clock uses a laser to launch cooled cesium atoms upward, as if they were water droplets from a fountain, so that the Doppler shift caused by the upward motion cancels out nearly all of the shift that occurs as they fall.
But nowadays cesium clocks can’t be improved much more. Tiny gains are increasingly difficult to achieve, and any gains we try to make now will take a long time. That’s because cesium clocks are pushing the limit of the other key metric we use to evaluate clocks: the stability of their frequency.
Frequency stability characterizes how clock frequency fluctuates over time. The bigger the frequency instability, the greater the frequency noise, so the clock frequency will sometimes be a bit higher and sometimes a bit lower than its average value.
Careful engineering can minimize most sources of frequency noise. But there’s a fundamental source of instability that is very difficult to overcome, because it comes from the probabilistic nature of quantum mechanics. To understand it, let’s go back to the basic operating principle of an atomic clock.
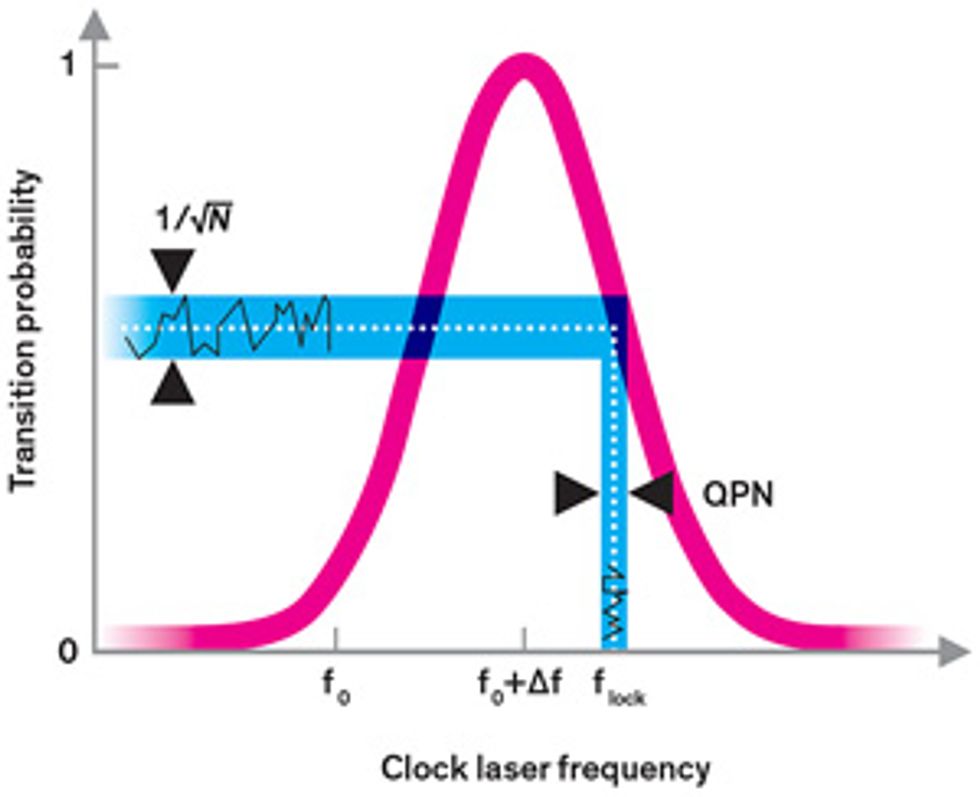
We typically excite the electrons in an atomic clock with radiation whose frequency doesn’t quite match the transition frequency. That’s because the probability that an electron will be excited follows a bell-curve-like distribution. On the sides of the bell curve, it’s easier to see whether a small change in frequency has occurred because it produces a more detectable effect, more dramatically increasing or decreasing the likelihood that an electron is excited [see illustration, "Finding the Frequency"]. Because of this, during the ordinary operation of an atomic clock, the clock radiation is set so that it has only a 50 percent probability of getting any given atom to make the clock transition. But even if the clock radiation frequency is set precisely at that point, an electron will be in either an excited or an unexcited state after it’s measured. The servo loop will then wrongly assume that the clock radiation frequency is either too high or too low and will introduce an undue frequency correction.
These miscorrections yield additional noise in the clock that we call quantum projection noise (QPN), and they are the main source of frequency instability in the best cesium clocks. Like many random sources of noise, the average level of QPN decreases with time. The longer you observe the clock, the more often the random upward shifts in frequency cancel out the downward shifts, and the noise eventually becomes negligible.
The catch is that this takes a long time in cesium: It takes about a day for the stability of the best cesium clocks to reach 2 parts in 1016 —their steady-state accuracy level. (Metrologists commonly measure quantities such as accuracy and stability in fractional units. For a cesium clock with a frequency of 9.2 gigahertz, an accuracy of 2 × 1016 —translates to an uncertainty of 1.8 microhertz in the frequency.)
You could run a series of experiments to make cesium clocks more accurate. But each measurement would have to consist of a lot of data taken over a very long time in order to minimize random fluctuations from measurement to measurement. In a series of experiments designed to push the clock accuracy down to 1 part in 1017, a 20-fold improvement, it could take an entire year just to make a single measurement.
Fortunately, there are other ways to minimize QPN. The noise is the same regardless of frequency, but its relative impact decreases the higher in frequency you go. And just as the average QPN decreases the longer you observe a clock, increasing the number of atoms you interrogate at the same time will boost the signal-to-noise ratio. The more you can sample in one go, the less uncertainty you’ll have in the number of atoms that made the clock transition.
Moving to higher frequencies is what motivated work on the optical atomic clock. The first of these clocks was developed in the early 1980s, and nowadays they can be built from any of a number of neutral or ionized versions of elements, including mercury, strontium, calcium, ytterbium, and aluminum. What they all have in common are relatively high resonance frequencies, which lie in the optical spectrum around several hundred thousand gigahertz—10,000 times cesium’s frequency. Using a higher frequency lowers the QPN, and it also lowers the relative impact of several factors that can shift the clock frequency. These include interactions with external magnetic fields coming from Earth or nearby metal (or, in Paris, the Métro lines). As an added bonus, if an optical clock is built with ions, those charged atoms can easily be trapped in an oscillating electric field that will cancel out most of their motion, effectively eliminating the Doppler effect.
But optical clocks have limitations of their own. If all other aspects of a clock are the same, the move to optical frequencies should lower the QPN to 0.01 percent of what it is in cesium. But many optical clocks are made with ions instead of neutral atoms, such as those used in cesium clocks. Because they’re charged, ions are fairly easy to trap, but they also easily push on one another when placed close together, creating motion that’s hard to control and causing a Doppler frequency shift. As a result, such clocks tend to use just one ion at a time and so are only about 20 times as stable and 25 times as accurate as the best cesium clocks, which can easily contain a million atoms. To get closer to the factor-of-10,000 boost in stability promised by optical clocks, we must find a way to boost the number of atoms in the optical clock, simultaneously interrogating many atoms so that the QPN averages out. And with the optical-lattice clock, researchers realized they could go quite big, measuring not just a handful of atoms but 10,000 or more at the same time.
It certainly isn’t easy. To build a clock out of 10,000 atoms, you must find a way to make an atomic ensemble that is both tightly confined (to minimize the Doppler effect) and very low in density (to minimize electromagnetic interactions among the atoms). The atoms in a typical crystal move too fast and interact too strongly to work, so the best way to proceed is to produce an artificial material with a lattice of your own creation.
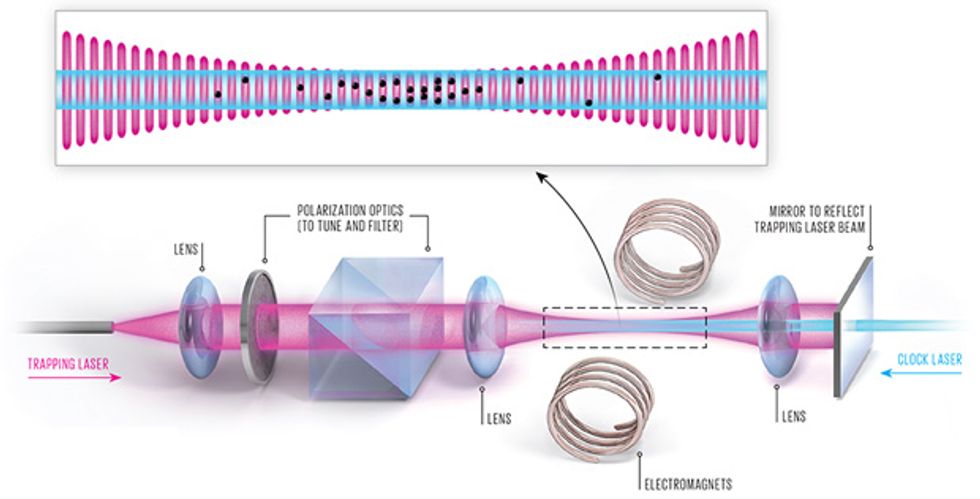
To build an optical-lattice clock, we start much the same way we do in many cold-atom experiments, with an ensemble of slow-moving, laser-cooled neutral atoms. We send these into a vacuum vessel containing a single laser beam that has been reflected back on itself. An interference pattern arises in the areas where the beam overlaps with itself, creating an optical lattice made of thousands of small “pancakes” of light. The atoms fall into the lattice like eggs into an egg carton because of a force that draws each of them toward a spot where the light intensity is at a maximum. Once the atoms are in place, we use a separate “clock laser” to excite the atoms so that we can measure the frequency of the clock transition.
The difficulty is that the clock atoms aren’t so easy to coerce into this lattice. Inexpensive lasers have outputs in the milliwatts. To create a lattice strong enough to trap and hold a neutral atom, you need several watts of light. Such a powerful laser beam, however, can shift energy levels in clock atoms, pushing their transition frequency far from their natural state. The amount of this shift will vary with the intensity of the trapping light, and that intensity is hard to control. Even with very careful calibration, this large frequency shift would render the clock much more inaccurate than even the very first cesium clocks.
Fortunately, physicist Hidetoshi Katori conceived a workaround in the early 2000s. When atoms are hit with the trapping light, the energy associated with each electron orbital decreases. Katori, then at the University of Tokyo, noted that each orbital will respond differently, with an energy shift that will depend on the wavelength of the trapping light. For a specific, “magic” wavelength, the shift of both orbitals will be identical, and so the energy difference between the two orbitals will be unchanged. This magic wavelength, where the clock frequency stays the same whether the atoms are trapped or not, is different for each element. For strontium, it’s 813 nanometers, in the infrared part of the spectrum. Ytterbium’s magic wavelength is 759 nm; mercury’s is in the ultraviolet part of the spectrum, at 362 nm.
When Katori made his proposal, my group at the Paris Observatory’s Systèmes de Référence Temps-Espace (LNE-SYRTE) department, which is responsible for maintaining France’s reference time and frequency signals, had already been investigating the use of strontium for optical clocks. We set to work almost immediately to see if we could make an optical-lattice clock using strontium, competing at first with just two other groups that had long-standing experience working with cooled strontium: Katori’s team in Tokyo and Jun Ye’s group at JILA, in Boulder, Colo. A decade and many projects later, other groups have built lattice clocks using strontium and ytterbium. More experimental projects using mercury or magnesium, which require still higher-frequency and less-well-developed lasers, are also in the works.
One of the key factors in making optical-lattice clocks more accurate over the past few years has been the development of clock lasers with very narrow spectra—essentially just a small spike at one particular frequency. We need these to effectively explore the region around the transition frequency of the clock, to see in fine detail how a slight shift in the clock frequency affects the transition probability.
The best way to make narrow-lined laser light is to feed it into a mirrored chamber called a Fabry-Pérot cavity. After bouncing back and forth up to a million times inside this cavity, light of any arbitrary wavelength will have interfered with itself and canceled itself out. Only laser light with a wavelength that is a unit fraction of the length of the cavity emerges.
While the cavity helps to filter out natural fluctuations in the frequency of a laser source, the technique isn’t perfect. The frequency of the clock laser that emerges from the cavity can wobble around because of thermal fluctuations that cause the cavity to slightly expand or contract.
But over the past few years, researchers have found ways to help mitigate this effect. Cavities were made longer, so the relative impact of a small change in length is smaller. Vibrations were damped. The cavities were also cooled to cryogenic temperatures, to limit tiny expansions and contractions due to thermal energy.
The net result was much more stable clock lasers. Nowadays, over the few seconds it takes to prepare and probe clock atoms, a 429-terahertz clock laser might drift in frequency by just 40 millihertz or so. For a typical cavity, with a length of a few dozen centimeters, that amounts to changes in its length of no more than a few percent of the size of a proton for the several seconds it takes to prepare and probe the atoms in the optical clock.
Largely due to this effort, the stability reached within one day with cesium clocks, or within a few minutes with optical-ion clocks, can now be reached in 1 second with an optical-lattice clock, close to the QPN limit. This improved stability makes the clock itself a tool. The less time you need to gather data to measure an atomic clock’s frequency with precision, the faster you can use the clock to run experiments to explore ways to make it better. Indeed, just three years after the first frequency stability improvements were demonstrated in optical-lattice clocks at the U.S. National Institute of Standards and Technology, these clocks took the lead for accuracy. The published record is now held by one of the strontium OLCs at JILA, which boasts an estimated accuracy of 6.4 parts in 1018.
A clock is only so good on its own. Evaluating one clock requires another, comparable clock to serve as a reference. When OLCs were first developed a decade ago, the initial comparisons were done between strontium OLCs and cesium clocks. These measurements were enough to establish the early promise of OLCs. But to truly ascertain the accuracy of an atomic clock, it’s crucial to directly compare two clocks of the same type. If they are as accurate as advertised, their frequencies should be identical.
So as soon as we had finished building one strontium optical-lattice clock in 2007, we began work on a second. We finished the second clock in 2011, and set to work making the first comparison between two optical-lattice clocks in order to directly establish their accuracy, without relying on cesium clocks.
Once a second clock is built, previously undetectable problems soon become apparent. And indeed, we soon uncovered flaws that had been overlooked. One was the influence of static electric charges that had become trapped on the windows of the vacuum chamber. We had to shine ultraviolet light on the windows to efficiently dislodge the charges.
In a paper that appeared last year in Nature Communications, we showed that our two strontium OLCs agree down to the 1 part in 1016 level, a solid confirmation that these clocks are more accurate than the best cesium clocks. Earlier this year, Katori’s team at the research institution Riken, in Wako, Japan, reported an agreement of a few parts in 1018 in similar clocks, this time enclosed in a cryogenic environment.
Incidentally, the frequency of an optical clock is so fast that no electronic device could possibly count its ticks. These sorts of clock comparisons rely on a new technology that’s still very much in development: the frequency comb. This instrument uses femtoseconds-long laser pulses to create a spectrum that consists of coherent, equally spaced teeth that span the visible and infrared spectrum. In effect, it acts like a ruler for optical frequencies.
The ability to perform comparisons between OLCs pushes us further along the road to redefining the second. Before a redefinition in the International System of Units can take place, a large number of laboratories must demonstrate not only that they can implement the new standard but also compare their measurements. Consensus is needed to establish that all the laboratories are on the same page. It is also necessary to ensure that the world can literally keep time: Coordinated Universal Time, the time by which the world’s clocks are set, and the International Atomic Time it’s derived from, are created by making a weighted average of a large number of microwave clocks around the world.
Cesium clocks are “networked” using the signals emitted by satellites and are compared by microwave transmission. This is good enough for microwave clocks but too unstable for distributing more-accurate optical-lattice clock signals. But soon, international comparisons of optical clocks will reach a new milestone. New fiber connections, built with dedicated phase-compensation systems that can cancel small timing shifts introduced by the lines, are now being constructed.
By the end of this year, thanks to a number of national and international projects, we expect to be able to start using such connections to make the first comparisons between optical-lattice clocks based at LNE-SYRTE in Paris and the Physikalisch-Technische Bundesanstalt, Germany’s national metrology center, in Braunschweig. A link to the National Physical Laboratory, in London, which has strontium- and ytterbium-ion clocks, is also set to be completed early next year. These efforts will pave the way for an international metrology network that could enable a new standard for the second.
In the meantime, scientists have already begun using optical-lattice clocks as a tool to explore nature. One focus has been on measuring the frequency ratio between two clocks that use different types of atoms. This ratio depends on fundamental physical constants, such as the fine-structure constant, which could reveal new physics if it turns out to vary in time or from place to place.
Astronomers may also benefit from optical clocks. Atomic clocks are used as a time reference in radio astronomy, allowing astronomers to combine the light collected by telescopes separated by hundreds or thousands of kilometers to produce a virtual telescope, with an angular resolution equivalent to that of a single telescope spanning that entire distance. As optical atomic clocks mature, they could enable a similar feat for optical telescopes.
And it’s not hard to imagine that optical-lattice clocks could offer new insight into the world beneath our feet. According to Einstein’s theory of general relativity, a clock sitting on a denser part of Earth will tick slower relative to one situated on a part that’s less dense. Although gravimeters can be used to measure gravitational force at any one point, measuring gravitational potential—which could shed light on different, deeper structures inside Earth—must be done by integrating the measurements of gravimeters at different points around Earth’s surface or by measuring the orbits of satellites. Metrologists and geodesists are now teaming up to understand what optical-lattice clocks will be able to offer. It’s possible that they could be used at different points around Earth to assist with oil detection, earthquake monitoring, and volcano prediction.
In the meantime, there is still work to be done to keep improving the stability and accuracy of OLCs. Recently, a large effort has been made to fight the effect of black-body radiation. This radiation is unavoidably emitted by any physical body with nonzero temperature, including the vacuum chamber that surrounds the clock atoms. When it interacts with the atoms it shifts the energy levels of the clock transition. This shift can be corrected after the fact, but a precise knowledge of the temperature and emissivity of the vacuum chamber must be acquired. It is also possible to enclose the atoms in a cryogenic environment or use an atomic species that is inherently less sensitive to black-body radiation, such as mercury, a route that our group is exploring.
Before the end of the decade, new generations of ultranarrow lasers are also likely to help push stabilities below 1 part in 1017 after a single second of data gathering. That will make it practical for us to achieve an accuracy below 10−18— more than 100 times the precision of cesium clocks. As OLCs become more accurate, the scope of applications will continue to expand.
Even if OLCs are wildly successful, we won’t abandon the cesium clock, which will remain more compact and less expensive to build. And in the future, OLCs may be supplanted by clocks of even higher frequencies that rely on energy transitions inside the atom’s nucleus instead of among the electrons in orbit around it. These nuclear transitions are mostly out of reach of current laser technology, although researchers are starting to explore them.
But before long we will see yet another time standard that could significantly influence the way we relate to our universe. Just as surely as time keeps on ticking, improvements in our ability to measure it will go on.
This article originally appeared in print as “An Even Better Atomic Clock.”
About the Author
Jérôme Lodewyck, an associate professor at France’s National Center for Scientific Research, enjoys doing battle with atoms, pinning down every factor that might affect their behavior. This compulsion came in handy in 2007, when he took a postdoctoral position at the Paris Observatory and was immediately assigned to build an optical-lattice clock from scratch. These clocks are now the world’s most accurate and could one day redefine the second.