Understanding the System
We are developing a tank fluid-level monitoring system. This system can be deployed in breweries, wineries, and other beverage facilities at the IoT edge to collect the status of the fluid levels and to notify technicians proactively if there are any issues (such as leaks). We have modified the system (Figure 1) to utilize the PMUT sensor that monitors the fluid level in the tank and periodically transmits measurements to a gateway device.
The ultrasonic sensor produces acoustic waves in the tank and then measures the waves that get reflected by the liquid, resulting in a small analog waveform that requires amplification. The time difference between sending the wave and the measured reflected wave is proportional to the distance to the liquid. An analog front-end (AFE) amplifies the MEMS waveform and converts the signal to an integrated voltage representing time-of-flight or twice the depth to the liquid. An analog-to-digital converter (ADC) circuit converts the voltage to digital as an input into the microcontroller that runs the software. The clock, PLL, and oscillator circuits are supporting modules to the digital circuitry and the bias current generator, voltage regulator, and bandgap reference are supporting modules to the analog circuitry. The RF transmitter sends the data to the gateway. The Arm® Cortex®-M3 microcontroller interfaces to the analog circuits and RF transmitter. In the future, we plan on adding a temperature sensor which necessitates a multiplexer, but for this whitepaper we will not implement those two elements.
Understanding the Sensor
Ultrasonic transducers use acoustic waves to detect the distance between the sensor and other objects. They operate by converting electrical energy into mechanical energy, and in most cases, converting mechanical energy back to electrical energy. It is this duality of function that allows them to produce pressure waves that travel to an object or interface and subsequently detect them when they are reflected back to the source. They are widely used in everyday applications, but have historically been bulkier, more power hungry, and more expensive than competing technologies. This has limited their use in, for example, consumer applications, but this is changing fast. New generations of miniaturized ultrasonic transducers coming to market consume up to an order of magnitude less power than their predecessors. There is no better example than the current development and implementation of PMUTs, which we use for the sensor in our system. A PMUT consists of a piezoelectric thin-film membrane (typically PZT or AlN material) suspended above a cavity. When an electric impulse is applied, the membrane vibrates to produce acoustic energy in the medium directly contacting it. At its designed resonant frequency, a PMUT can produce a substantial amount of energy at very low power. Figure 2 shows a representative cross section of a PMUT, where the membrane thickness and diameter can be tuned to optimize the resonant frequency for a given medium. PMUTs are produced using well-established silicon semiconductor fabrication processes. Unlike many competing technologies, this allows them to be used in very high-volume applications at low costs, and more importantly, to be seamlessly integrated with CMOS to provide complete sensing systems on a chip.
Simulating the PMUT using Finite Element Analysis
As a first step in the PMUT design, we simulate the PMUT using a simulation technique called finite element analysis (FEA). By using FEA, intricate differential equations that describe the structure’s behavior can be converted into algebraic expressions, which in turn can be solved numerically. FEA can be used several ways in our design: to explore design concepts, perform functional verification of design performance, and to optimize the design. FEA can explore the real world variations in non-ideal geometric shapes, fabrication processing, and material properties and it is well suited to problems with complex boundary conditions. FEA tools rely on dividing the simulated structure into low-order finite elements or mesh. This process is assisted by auto-mesher functions that partition the structure efficiently. By refining the meshing where needed, the designer can get a set of accurate simulation results. By combining the mesh with other information from the electrical, mechanical, and thermal domains, coupled field modules can be used to simultaneously solve for electrostatics, coupled electro-mechanics, piezoelectric, piezoresistive, damping effects, and other characteristics.
Many important device characteristics can be simulated for ultrasonic sensors, including:
• Electrical impedance
• Mode shapes
• Pressure and displacement levels
• Beam patterns
• Directivity index
• Efficiency
• Pulse-echo response
• Crosstalk
• Bandwidth
• Material characteristics
• Mechanical shocks
• Bondline effects.
We utilize a powerful cloud-enabled, multi-physics FEA tool called OnScale, which provides all the capabilities mentioned above and executes them on a massively parallel Cloud infrastructure to allow design studies to be completed in hours instead of weeks.
Designing the Sensor
The nature of piezoelectric ultrasonic transducers presents a unique set of challenges to solve using simulation techniques such as FEA. One of the most fundamental challenges is the relative size of the computational domain required. Accurately capturing the small spatial gradients in stress created as the wave propagates demands a fine mesh (such as 8-12 elements per wavelength) to be deployed over a long path (such as 10-250 wavelengths). The result is a large number of elements needed to generate efficient simulation grids. OnScale is uniquely suited for models of this size due to its highly efficient solver and advanced hybrid meshing techniques. The PMUT used for this effort is modeled as a single 3D transducer with a nominal cavity width of 400 um, a top electrode diameter of 200 um, and a cavity depth of 40 um. The PMUT is excited with a series of voltage pulses applied to the electrode on top of the membrane. Figure 3 shows how the membrane deforms when a series of pulses at is applied at 32 V. The deformation is exaggerated for clarity.
To optimize this design, we need to maximize the mechanical energy received by the PMUT after reflection off of the fluid surface. We do this by building a design of experiments (DoE) that covers enough of the design space to contain our optimal solution. In this case specifically, we vary the design parameters (Table 1) to determine the best design.

Both the piezoelectric layer thickness and the membrane thickness are swept from 1.0 to 2.5 μm in 0.1 μm steps, yielding a total of 256 designs to be simulated. A subset of the results is shown in Figure 4, where resonant frequency is plotted against the swept parameters. These results inform the optimal dimensions of the design for our given environmental conditions prior to prototyping. In this case, the simulations indicate that power of the reflected wave is optimal at lower frequencies due to losses in air. We choose a piezoelectric layer thickness of 1.2 μm and a membrane thickness of 1.2 μm, which yields a low resonant frequency of 122 kHz, while keeping within the limits imposed by the manufacturing process. A design space of this size would be difficult to explore with a legacy FEA package, which is why OnScale was chosen for this analysis.
Designing the Analog Front-End
Figure 5 shows the analog front-end used in this design. The PMUT is schematically captured in S-Edit using a voltage source with the properties and parameters that match the output of the FEA study.
The time-of-flight function begins when the microcontroller sets the SR latch, which begins accumulating charge on a sample-hold integrator. At the same time, a series of pulses is produced by the microcontroller at the designed resonant frequency of the PMUT (122 kHz). The pulse is amplified to 32 V using a charge pump DC-DC converter and a digital level-shifter because the core power voltage is 2.5 V and it has to be raised to 32 V as required by the PMUT. The transducer receives the signal pulses, creating a pressure wave in the tank that is reflected back at the fluid interface (Figure 6). This reflected wave is sensed by the PMUT, creating a voltage signal on the membrane with a peak amplitude on the order of 500 μV that is delayed based on the how long it takes for the pressure wave to travel to the top of the liquid level and be reflected back to the PMUT.
An instrumentation amplifier, with a gain of 70 dB, amplifies the PMUT signal and feeds it to a Schmitt trigger. The Schmitt trigger, with built-in hysteresis, resets the SR latch when the reflected amplified signal rises above the threshold voltage (VREF) of 1.25 V. The latch reset also locks the sample-hold integrator, which has now accumulated charge on its output capacitor during the time it took for the pressure wave to traverse the air volume of the tank and return to the PMUT. An ADC before the microcontroller converts the voltage output of the integrator to a digital value that is a linear measure of the time-of-flight, and by subtraction, the fluid-level inside the tank.
Performing Initial System Simulation
When launching the simulation, S-Edit creates the complete Verilog-AMS netlist and passes it to T-Spice. T-Spice automatically adds analog/digital connection modules and then partitions the design for simulation. T-Spice simulates the analog (SPICE and Verilog-A) and sends the RTL to ModelSim® for digital simulation. Both simulators are invoked automatically and during simulation the signal values are passed back and forth between the simulators whenever there is a signal change at the analog/digital boundary. This means, that regardless of the design implementation language, the designer drives the simulation from S-Edit and the design is automatically partitioned across the simulators. Then, the designer can interact with the results using the ModelSim and T-Spice waveform viewers. Figure 7 shows the results of the simulation.
The waveform shows the high voltage pulse at 122 kHz (green). Next, the input to the instrumentation amplifier is plotted (red) with the PMUT response occurring around 1.2 ms after the initial pulse. Assuming a sound speed of 343 m/s in air, this corresponds to a fluid level 21 cm below full. The third waveform (purple) shows the output of the SR latch, which triggers when the PMUT output voltage exceeds ~400 μV (before amplification). Lastly, the output of the integrator is plotted (blue), showing a linear increase in voltage until the SR latch triggers the integrator to hold. The output is converted to digital by an 8-bit ADC before being sent to the microcontroller for calculation of the fluid level. For this design, the total tank depth is assumed to be 2.1 m. The maximum time-offlight can then be calculated to be 12.2 ms, which subsequently yields an integrator output of 2.17 V. This is close to the maximum input voltage of the chosen ADC (2.2 V), as designed. For different size tanks, the gain of the instrumentation amplifier can be adjusted accordingly.
Developing the Software
The software running on the microcontroller includes code to periodically convert the sensor output into fluid depth and to report any significant fluid level change to the monitoring system. Given that the integrator and ADC are approximately linear, the ADC output can be converted to time using a linear slope and intercept. These values are initially simulated and then verified through measurement of the analog simulation results. The time-of-flight is converted to air level by multiplying by the speed of sound in air (343 m/s). Finally, fluid level is derived as the total tank depth minus the air level.
Performing actual System Simulation
Because we already verified the MEMS transducer, and we want to significantly save simulation time, we use a stand-in Verilog behavioral model (Figure 8) of the sensor that samples data using discrete simulation time steps instead of continuous analog sampling.
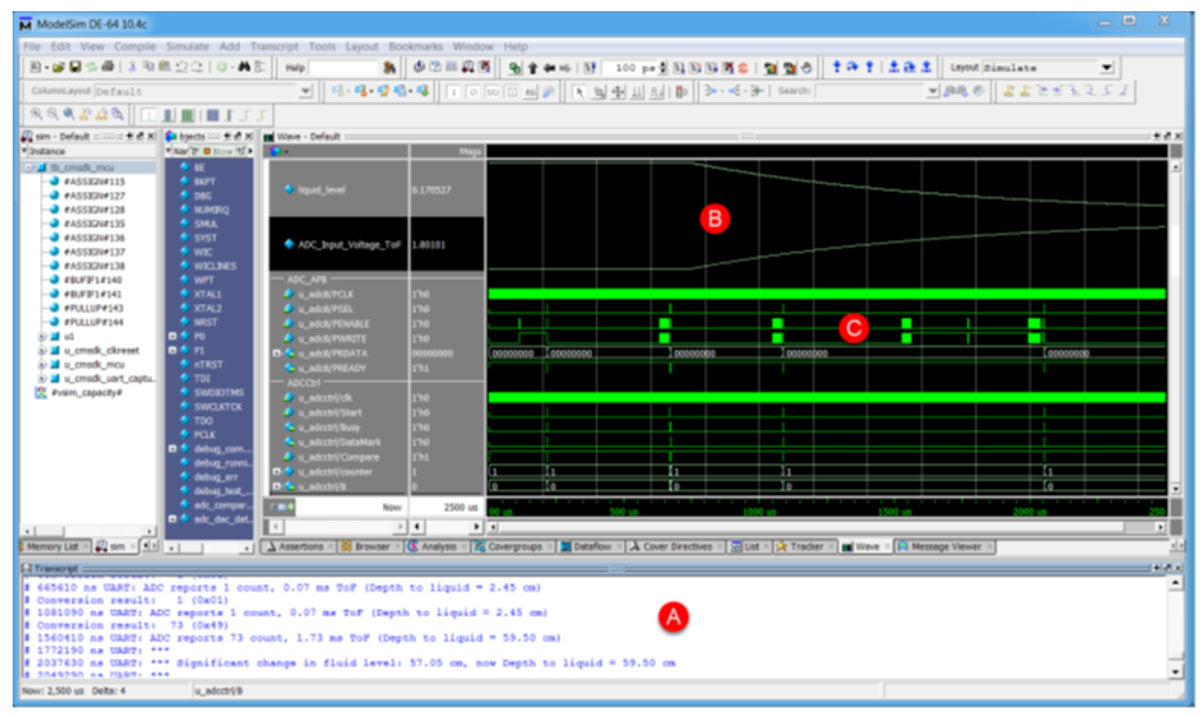
This model closely matches the analog sensor behavior, but samples the data every 1 us for faster system simulation, even though the ADC takes 12us for each conversion. Figure 9 shows the system simulation results. The transcript (A) displays the liquid level change warning and the waveforms show the liquid level and acoustic sensor values corresponding to the leak (B). The system spends most of the simulation time asleep, waking up to take depth readings periodically (C).
Next Steps
Some of the next steps are to flesh out the analog section, add an RF transceiver, and add a communication block and a device ID to the design in order to connect to the Internet. In addition, developing sophisticated software for the system and for the Web opens the doors to many possibilities, including potentially: two-way communication (directing the system to act), over-the-air software updates, preventative maintenance, and Cloud services. We also might move forward with adding a temperature sensor to the system to better calibrate the measurements. Look for future whitepapers on developing, implementing, and verifying this IoT system. To learn more about the Tanner solution, visit https://www.mentor.com/tannereda/
Click the link to download OnScale From Proof of Concept to Product Design of a MEMS Sensor eBook https://onscale.com/whitepapers/designs-of-a-mems-sensor/
Create your Free Account and start accelerating your research now.