Cracking GO
Brute-force computation has eclipsed humans in chess, and it could soon do the same in this ancient Asian game


In 1957, Herbert A. Simon, a pioneer in artificial intelligence and later a Nobel Laureate in economics, predicted that in 10 years a computer would surpass humans in what was then regarded as the premier battleground of wits: the game of chess. Though the project took four times as long as he expected, in 1997 my colleagues and I at IBM fielded a computer called Deep Blue that defeated Garry Kasparov, the highest-rated chess player ever.
You might have thought that we had finally put the question to rest—but no. Many people argued that we had tailored our methods to solve just this one, narrowly defined problem, and that it could never handle the manifold tasks that serve as better touchstones for human intelligence. These critics pointed to weiqi, an ancient Chinese board game, better known in the West by the Japanese name of Go, whose combinatorial complexity was many orders of magnitude greater than that of chess. Noting that the best Go programs could not even handle the typical novice, they predicted that none would ever trouble the very best players.
Ten years later, the best Go programs still can't beat good human players. Nevertheless, I believe that a world-champion-level Go machine can be built within 10 years, based on the same method of intensive analysis—brute force, basically—that Deep Blue employed for chess. I've got more than a small personal stake in this quest. At my lab at Microsoft Research Asia, in Beijing, I am organizing a graduate student project to design the hardware and software elements that will test the ideas outlined here. If they prove out, then the way will be clear for a full-scale project to dethrone the best human players.
Such a result would further vindicate brute force as a general approach to computing problems, if further vindication were needed. Even now, the method is being applied to such forbidding challenges as protein folding, scheduling, and the many-body problem.
Many of the early computer-chess researchers hailed from the fields of psychology or artificial intelligence and believed that chess programs should mimic human thinking. Specifically, they wanted computers to examine only playing sequences that were meaningful according to some human reasoning process. In computer chess this policy, known as selective search, never really made progress. The reason is that humans are extremely good at recognizing patterns; it is one of the things that we do best.
It was only in the late 1970s, with the success of Northwestern University's Chess 4.x program, written by David Slate and Larry Atkins, that the engineering school of thought became dominant. The idea was to let computers do what they do best, namely, calculate. A simple legal-move generator finds all the permissible moves in a position, considers all the possible responses, and then repeats the cycle. Each cycle is called a ply, each generation of new possibilities is called a node—that is, a branching point in a rapidly widening tree of analysis. The branches terminate in “leaf,” or end positions.
Carried to its logical extreme, the tree would grow until it exhausted every legal continuation, leaving the program nothing to do but examine the end positions to see which of them were wins—that is, checkmates—and which were draws, then work backward along the branching structure to choose the line that led to the best outcome, assuming that both sides play perfectly. Such exhaustive analysis is impractical, though, because it would produce a tree containing about 1060 positions. That's about a thousand times the number of hydrogen atoms in the sun.

There is, however, a course midway between selectivity and exhaustiveness. Instead of analyzing to the end, the program can merely look a few moves further ahead than a human could manage. Deep Blue typically looked 12 plies ahead in all variations (and 40 or more plies in selective lines), generating around 170 million leaf nodes per second. Next, the program would evaluate each of these positions by counting “material,” that is, the standard values of the chess pieces. For example, a pawn is worth one point, a knight or bishop three, and so on. Then it added points for a range of positional factors, chosen with the help of human grandmasters.
The resulting evaluation function probably was no better than a middling amateur's ability to grade a single position. But by grading 200 million of them, it was able to do very well indeed. Just ask Kasparov.
This substitution of search for judgment is the essence of the brute-force method, and it turned out to have two critical advantages over selective search. To begin with, the program became easier to write, had far fewer bugs, and did not have so many blind spots. And crucially, the program played significantly and measurably better as the processing power increased, once the switch to brute force had been made.
Slate and Atkins believed their program was playing at only Class C level—that is, about the level of the typical avid tournament player, who is rated between 1400 and 1600 on the U.S. Chess Federation's rating scale. However, when they moved their program to a supercomputer, it shocked everyone by winning a tournament among Class A players, with ratings between 1800 and 2000. A Class A player is good enough to beat a Class C player 9 times out of 10, on average.
Moving to a supercomputer made this enormous difference because it allowed the program to look just a little further ahead. Detailed measurements later showed that when a brute-force program searched just one ply deeper, its strength improved by between 200 and 300 rating points. When two players are separated by that big a gap, the higher-rated player will win, on average, 4 out of 5 games.
It was this almost linear relationship between search depth and playing strength that first made me believe chess could be solved. I wondered whether the relationship would continue all the way up to the World Champion level—about 2900 on the Chess Federation's scale. In the end, this conjecture proved to be partly true. That is, the program did continue to play better as search depth increased, but additional gains in rating could also be achieved by improving the evaluation function and the selectivity of its search.
Go is played on a board crisscrossed by 19 vertical and 19 horizontal lines whose 361 points of intersection constitute the playing field. The object is to conquer those intersection points.
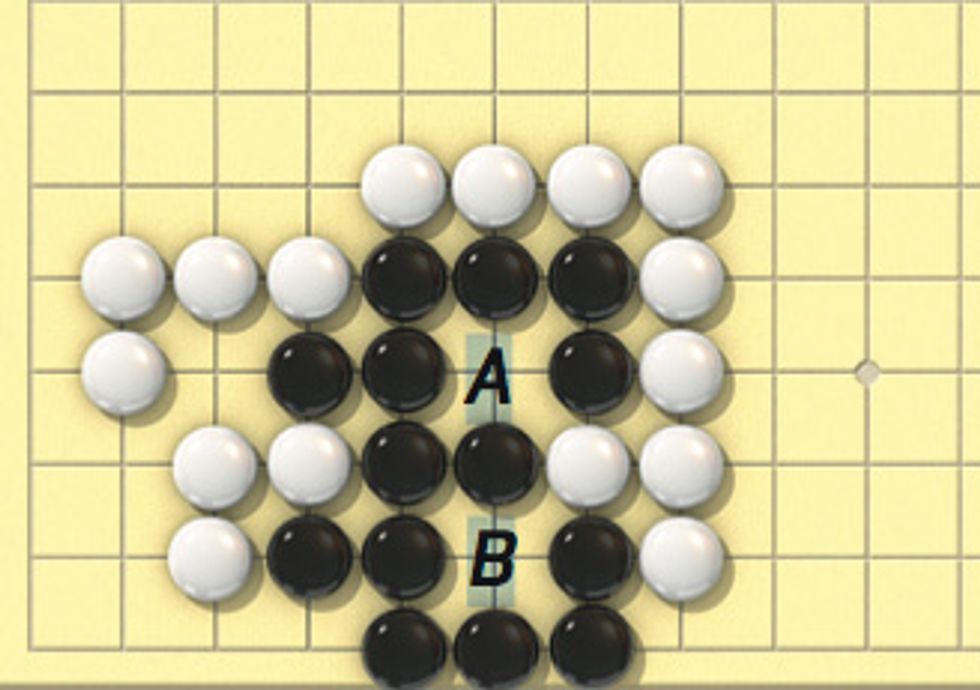
A player makes a move by placing a lozenge-shaped “stone” on an intersection, then the other player counters, and the two alternate moves. Players capture enemy stones by surrounding them, that is, by removing their “liberties,” which consist of either the vacant points adjacent to a stone itself or to friendly stones to which it is itself connected (see illustration, “The Goal of Go”). When no more moves are possible, the players count up the intersection points they control, and the player with the most points wins.
All the leading Go programmers today belittle brute force. In this they resemble the computer chess experts of 40 years ago. Selective search dominated thinking on computer chess from the late 1940s to the late 1970s, and that mind-set prevented any program from advancing beyond the level of a Class C player.
Go does, however, present two real problems, both having to do with the amount of searching the program must perform.
The first problem is the tree of analysis. Because Go offers more possibilities at every turn, the tree is far bigger for Go than for chess. At the start of the game, the first player can place a stone on any one of 361 positions, the second player has 360 choices, and so on. A typical game lasts about 200 moves, so it averages at least 200 move choices per turn—nearly 10 times as many as in the average chess position.
The second problem is the evaluation of the end positions. In Go you can't just count up stones, because you have to know which stones are worth counting. Conquered territory is defined as board space occupied or surrounded by “living” stones—stones the opponent cannot capture by removing their liberties. Before you can count a stone as live, you have to calculate several moves ahead just to satisfy yourself that it is really there in the first place.
Put these two problems together and you get a computational problem that at first glance seems intractable. But there are ways to engineer around it.
Let's start with the problem of the exploding tree of analysis. If we assume that the program must consider every possible continuation that could arise 12 plies into the future, as Deep Blue did in chess, you might expect to have to search a million times as fast. But we don't really need to pay that high a price, because there are ways to prune the tree of analysis.
One old standby, implemented in all chess programs, is called alpha-beta pruning, and it works by curtailing the examination of a move the moment it becomes clear that another move must be better. Let's say the program is comparing move A with move B, and it already knows that A leads to an advantage. If it finds, early on, that move B allows the other side to obtain a draw at the very least, then the program can cut off its analysis, saving a lot of time.
Alpha-beta pruning reduces the effective branching factor to about the square root of the number of move choices. For example, to look ahead 12 plies in pure brute-force mode, you would need to search only about 4 billion positions, or 4 x 109, instead of 3812—or 1019—positions.
A newer way to cut back the overgrowth—null-move pruning—was not implemented in Deep Blue, even though one of its inventors, Murray Campbell, was a key member of the Deep Blue team. The algorithm performs a kind of thought experiment, asking how the position would look if you were to give up the right to move for one turn, thus allowing your opponent to make two moves in a row. If after that enormous sacrifice you still have a good position after a relatively shallow search, then the algorithm can stop its analysis right there. It has identified a cutoff point—a point at which the branch can be pruned, thus saving the labor of going through all the other possible responses.
Imagine that the program examines a line in which it has just won the opponent's queen—giving it an enormous material advantage—and the opponent has responded. Now the program asks: If I do nothing, can my opponent hurt me after, say, n–2 plies—where n is the number of plies I would have searched after a legal instead of a null move? If the answer is no, the program concludes that it has indeed won an entire queen for nothing, that its position is likely won, and that no further analysis is necessary. This dividend is well worth the shallow “n–2 ply” search the computer has invested.
In computer chess, the main risk in null-move pruning comes from the null move (or pass) itself, which is illegal in chess. Because it is illegal, certain positions that could be defended by a pass must lose; the null-move trick can cause a program to ignore this condition. In Go it doesn't matter, though, because players are allowed to make passes.
Null-move pruning was first proposed as a fairly conservative technique, curtailing the depth of search only by n–1 plies, but experimenters soon found that n–2 or even n–3 reductions sometimes gave good results. Even better performance comes from applying null-move pruning inside the reduced-depth search itself. Such “recursive null-move pruning,” when coupled with standard alpha-beta pruning, appears to reduce the branching factor to about the square root of the square root of the number of move choices. This means that recursive null-move pruning can keep the analysis tree from growing any faster in a Go program than it would in a chess program that did not use null-move pruning.
The upshot is that a machine searching no faster than Deep Blue did 10 years ago could go 12 brute-force plies deep in Go (with additional selective search extensions). It does so, however, without making a full and proper evaluation of the resulting positions, as it could do for chess.
Yet another time-saving technique emulates human thought (for a change). When human players search through the Go game tree, they generally check the live-or-dead status of each stone only once, then in effect cache the result in their memories. In other words, they don't check again unless they have good reasons to do so. The point of caching is to fetch often-used information rather than recalculate again and again.
The idea has been tried in computer chess, in the “method of analogy” algorithm, which reuses conclusions reached in one branch of analysis when similar positions arise in other branches. It reduces the search tree by a factor of three or four, but unfortunately the operations needed to cache, retrieve, and apply the conclusions slows the program by the same proportion. To wring a net gain out of the method, therefore, the slowdown must be contained, for instance, by using special-purpose hardware to do the computation or by finding new ways to chop the search tree even further.
Think of the tree again. What the method of analogy basically does is to take an entire branch from one part of the tree and graft it to another. Suppose that early on the program discovers a sequence in which white can win in just one ply, by capturing black's queen with a bishop. The program will then cache that sequence and apply it to latter parts of the search tree, provided that nothing major has happened in the meantime (like losing a piece) and that the bishop can still capture the queen.
In chess, this method of analogy works only for very short branches or for branches that contain mostly “forced” moves, that is, checks, check evasions, and captures. However, if the branches contain more than a ply or two of nonforcing moves (which present far more possibilities for calculation), then the program's accounting system breaks down.

The reason has to do with the nature of the accounting system, which consists of a map of on/off bits that tracks the “to” and “from” squares of each chess piece. The program uses this bitmap to decide whether anything has happened to invalidate the graft—for instance, by making the winning move in a grafted branch illegal or providing the losing side with a way out of a sequence of forced moves. It turns out in chess that if grafted branches contain more than one ply of nonforcing moves, the bitmaps will quickly cover most of the board, the accounting system will become unmanageable, and the grafting operation will fail.
In Go, however, the method of analogy should be much more useful. Because the board is so large (19 by 19 versus 8 by 8 in chess), a battle typically occurs in a relatively small part of it, so the bitmaps will mostly have “off” bits, making it more likely for them to be useful. Also, the program can generally reuse the maps many more times than in chess, because each of the many local battles tends to be unaffected by battles elsewhere. Therefore, the program should be able to graft deep branches—the kind needed to decide life-and-death questions—from one part of the game tree to another.
This ability to answer life-and-death questions cheaply is vital if the brute-force approach is to work. To determine whether a group of pieces will live or die the program may have to search from 1000 to 1 000 000 positions. That wouldn't be so bad, really, if it were the extent of the problem. It isn't. In a typical game, we may easily have more than 10 such problems on the board at the same time, and the status of one group can affect that of its neighbors—like a cowboy who points a revolver at another cowboy only to find himself covered by a rifleman on a roof. Such interactions can complicate the problem by something on the order of taking 1 million to the 10th power—enough to stretch a calculation lasting a microsecond into one vastly dwarfing the age of the universe.
This is where the bitmaps we mentioned earlier come to the rescue. They make it easy to tell when maps do and do not intersect and also allow caching to work, thereby drastically reducing the cost of dynamic search required for proper evaluation of positions. It is conceivable that with caching techniques, including but not limited to the method of analogy, it may take no more than 1000 to 1 000 000 nodes (or one individual life-and-death decision tree) of dynamic search to properly evaluate an end position. Although that's more expensive than in the case of chess, it's manageable.
What, then, can we expect from the hardware? Deep Blue used 0.6-micrometer CMOS technology, kind of creaky even in 1997. Each of its 480 custom-designed processors searched up to 2.5 million positions per second. The theoretical peak speed was more than 1 billion positions per second, but the sustained speed was only 200 million positions per second because of communication overhead, load-balancing issues, and implementation inefficiency.
Today 45-nanometer process technology is just getting into production. With it, a machine searching as fast as Deep Blue could easily fit on a single chip. In fact, with gains expected from technology and from optimization of chip architecture, a single-chip machine could actually be more than 100 times as fast as Deep Blue. If we then made 480 copies of that monster chip and integrated them all in a parallel architecture, we could get at least another 100-fold increase in computational power. On top of that, in 10 years Moore's law is expected to present us with still another 100-fold speedup.
Put it all together and you should be able to build a machine that searches more than 100 trillion positions per second—easily a million times as fast as Deep Blue.
That would be enough to build a tree of analysis for Go as big as Deep Blue's was for chess and to evaluate all its end positions properly. If we assume the top Go players calculate about as deeply as the top chess players do, the result should be a machine that plays Go as well as Deep Blue played chess.
Well enough, that is, to beat any human player.
My gut feeling is that with some optimization a machine that can search a trillion positions per second would be enough to play Go at the very highest level. It would then be cheaper to build the machine out of FPGAs (field-programmable gate arrays) instead of the much more expensive and highly unwieldy full-custom chips. That way, university students could easily take on the challenge.
At Microsoft Research Asia we are seeding university efforts in China with the goal of solving some of the basic problems. Whether these efforts lead to a world-champion Go machine in the next decade remains to be seen. I certainly wouldn't bet against it.
About the Author
Feng-Hsiung Hsu earned a Ph.D. in computer science at Carnegie Mellon University, Pittsburgh, where he and fellow students designed the first grandmaster-level chess machine. Then he moved to IBM to develop its successor, Deep Blue, which beat World Champion Garry Kasparov in 1997. Hsu now manages the platforms and devices center of Microsoft Research Asia, in Beijing.
To Probe Further
For a full account of the IBM project to build a chess machine, see Behind Deep Blue: Building the Computer That Defeated the World Chess Champion, by Feng-hsiung Hsu, Princeton University Press, 2004.
To experiment with a Go program, readers can download GNU Go at https://www.gnu.org/software/gnugo. Offered by the Free Software Foundation, in Boston, this free program has performed well in recent computer Go events.


