Gilbert Strang, author of the classic textbook Linear Algebra and Its Applications, once referred to the fast Fourier transform, or FFT, as “the most important numerical algorithm in our lifetime.” No wonder. The FFT is used to process data throughout today’s highly networked, digital world. It allows computers to efficiently calculate the different frequency components in time-varying signals—and also to reconstruct such signals from a set of frequency components. You couldn’t log on to a Wi-Fi network or make a call on your cellphone without it. So when some of Strang’s MIT colleagues announced in January at the ACM-SIAM Symposium on Discrete Algorithms that they had developed ways of substantially speeding up the calculation of the FFT, lots of people took notice.
“FFTs are run billions of times a day,” says Richard Baraniuk, a professor of electrical and computer engineering at Rice University, in Houston, and an expert in the emerging field of compressive sensing, which has much in common with the approaches now being applied to speed up the calculation of FFTs.
Efforts to improve the calculation of Fourier transforms have a long and generally overlooked history. While most engineers associate the FFT with the procedure James Cooley of IBM and John Tukey of Princeton described in 1965, specialists recognize that it has much deeper roots. Although he never published it, the renowned German mathematician Carl Friedrich Gauss had worked out the basic approach, probably as early as 1805—predating, remarkably enough, even Fourier’s own work on the topic.
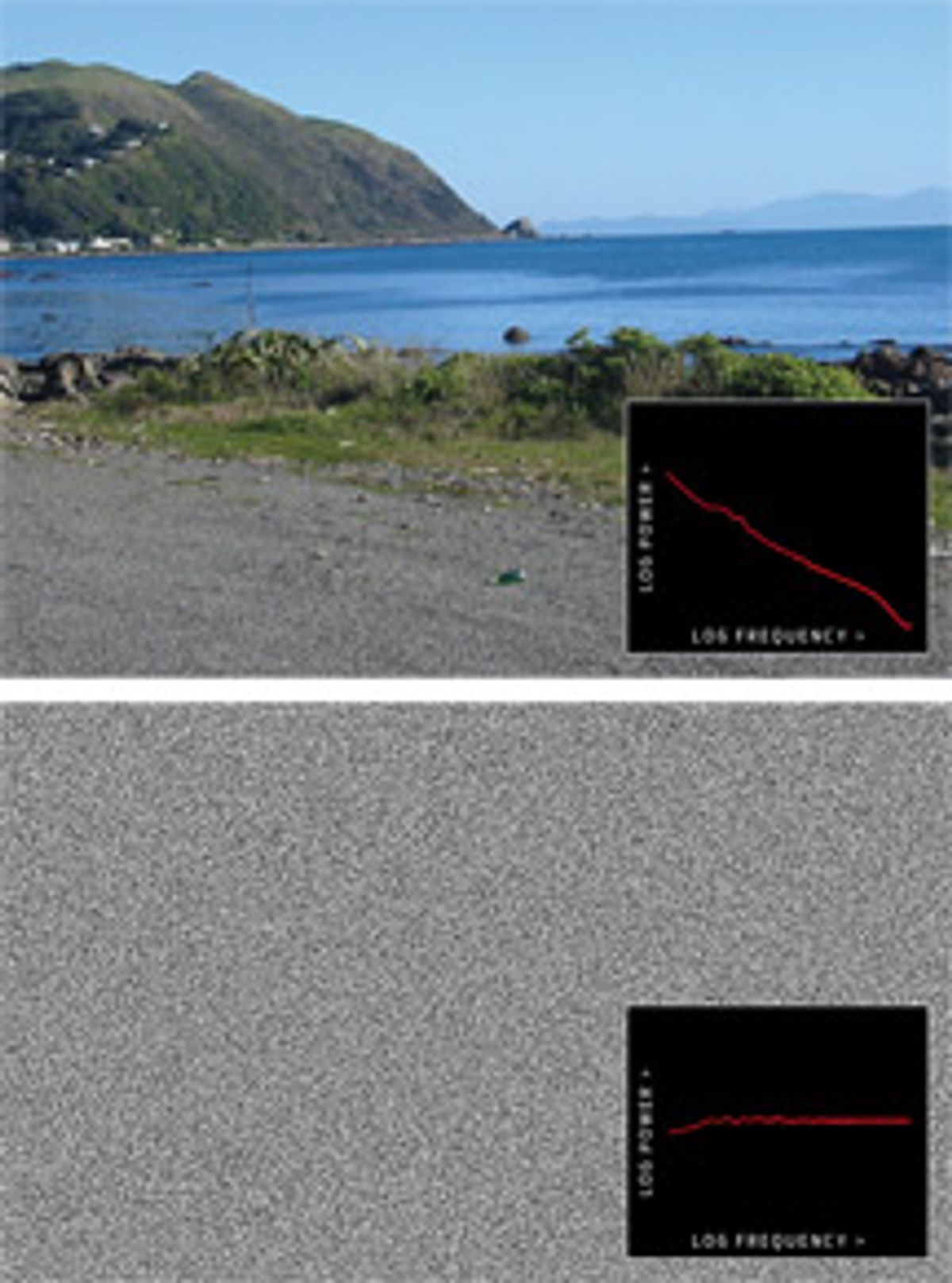
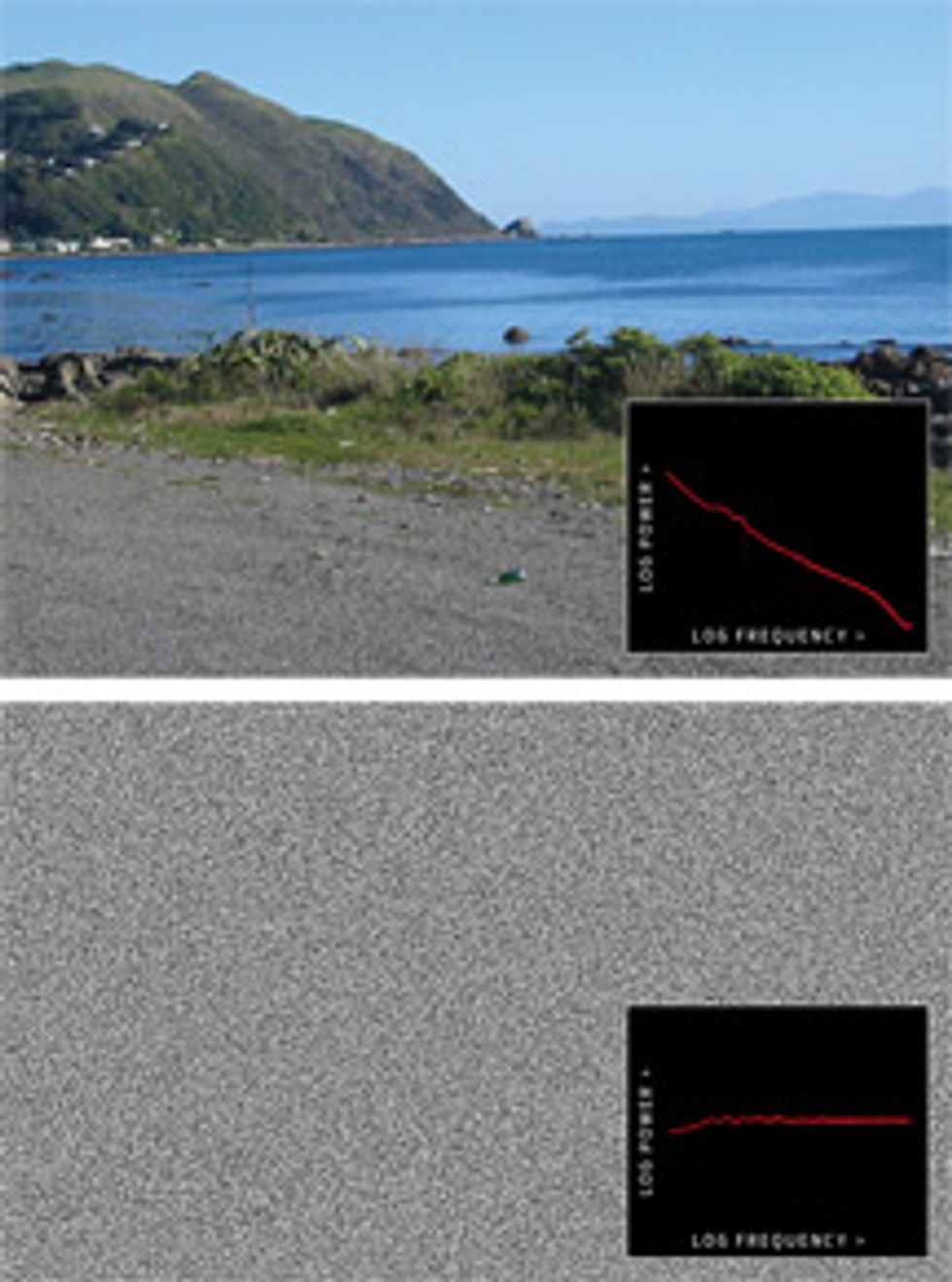
Given that great mathematical minds have been thinking about how to speed up this particular calculation for more than two centuries, how is it that progress is still being made? The fundamental reason is that the newer methods are tailored to run fast for only some signals—ones that are termed “sparse” because they contain a relatively small number of frequency components of significant size. The traditional FFT takes the same amount of computational time for any signal.
“Certainly there are applications where you need to run the full FFT because the data are not sparse at all,” says Piotr Indyk of MIT’s Computer Science and Artificial Intelligence Laboratory, who developed the new algorithms in collaboration with his colleague Dina Katabi and two students, Haitham Hassanieh and Eric Price. Fortunately, many real-world signals satisfy this sparsity requirement.
“Most signals are sparse,” says Katabi, who points out that when you send, say, a video file over wireless channels, transmitting only a few percent of the frequency content is typically sufficient—and in line with the sparsity levels that her group’s new algorithms handle well. Baraniuk adds that the frequency content of many natural signals, be they astronomical images or bird chirps, tends to be concentrated among the lower frequencies. “Sparsity is everywhere,” he says.
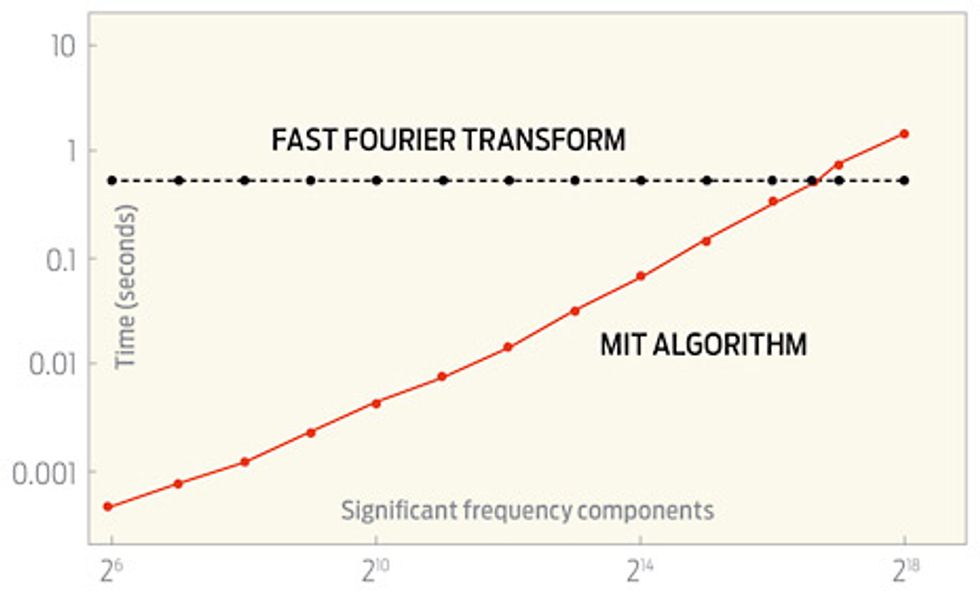
The newest MIT algorithm, which is described in a soon-to-be-published paper, beats the traditional FFT so long as the number of frequency components present is a single-digit percentage of the number of samples you take of the signal. It works for any signal, but it works faster than the FFT only under those conditions, says Indyk.
Experts say the new algorithms coming from MIT represent considerable progress. “They’ve added some very smart ideas to the recipe,” says Mark Iwen of Duke University, in Durham, N.C., who had earlier worked on the same problem with Anna Gilbert and Martin Strauss at the University of Michigan. The time it takes Iwen’s best FFT algorithm to run increases in proportion to the fourth power of the logarithm of the number of samples, whereas the newest MIT algorithm has a run time that’s proportional to just the first power of that number. “Removing those log factors is incredibly difficult,” says Iwen, who also credits the MIT group for coming up with impressively fast computer implementations of their new algorithms.
Indyk points out that the library of code his group (and many engineers) uses to calculate the traditional FFT was released in the 1990s—three decades after Cooley and Tukey had worked out the basic computer procedures required. “We don’t plan to spend 30 years developing a library,” he says. “We plan to release our prototype code soon; researchers can just play with it and see what happens.” Then, in something like six months, the MIT group should be able to provide a well-tested, portable library.
Why so long? “Developing decent code takes time,” Indyk says. But there’s another thing, he points out, that’s bound to delay their release of a well-tested software library: “Every month or two we have a new idea.”
Special thanks to Steve Haroz for the images and their Fourier transform analysis.
The graph in this story was corrected on 27 February.