The Femtojoule Promise of Analog AI
To cut power by orders of magnitude, do your processing with analog circuits

Machine learning and artificial intelligence (AI) have already penetrated so deeply into our life and work that you might have forgotten what interactions with machines used to be like. We used to ask only for precise quantitative answers to questions conveyed with numeric keypads, spreadsheets, or programming languages: "What is the square root of 10?" "At this rate of interest, what will be my gain over the next five years?"
But in the past 10 years, we've become accustomed to machines that can answer the kind of qualitative, fuzzy questions we'd only ever asked of other people: "Will I like this movie?" "How does traffic look today?" "Was that transaction fraudulent?"
Deep neural networks (DNNs), systems that learn how to respond to new queries when they're trained with the right answers to very similar queries, have enabled these new capabilities. DNNs are the primary driver behind the rapidly growing global market for AI hardware, software, and services, valued at US $327.5 billion this year and expected to pass $500 billion in 2024, according to the International Data Corporation.
Convolutional neural networks first fueled this revolution by providing superhuman image-recognition capabilities. In the last decade, new DNN models for natural-language processing, speech recognition, reinforcement learning, and recommendation systems have enabled many other commercial applications.
But it's not just the number of applications that's growing. The size of the networks and the data they need are growing, too. DNNs are inherently scalable—they provide more reliable answers as they get bigger and as you train them with more data. But doing so comes at a cost. The number of computing operations needed to train the best DNN models grew 1 billionfold between 2010 and 2018, meaning a huge increase in energy consumption And while each use of an already-trained DNN model on new data—termed inference—requires much less computing, and therefore less energy, than the training itself, the sheer volume of such inference calculations is enormous and increasing. If it's to continue to change people's lives, AI is going to have to get more efficient.
We think changing from digital to analog computation might be what's needed. Using nonvolatile memory devices and two fundamental physical laws of electrical engineering, simple circuits can implement a version of deep learning's most basic calculations that requires mere thousandths of a trillionth of a joule (a femtojoule). There's a great deal of engineering to do before this tech can take on complex AIs, but we've already made great strides and mapped out a path forward.
AI’s Fundamental Function
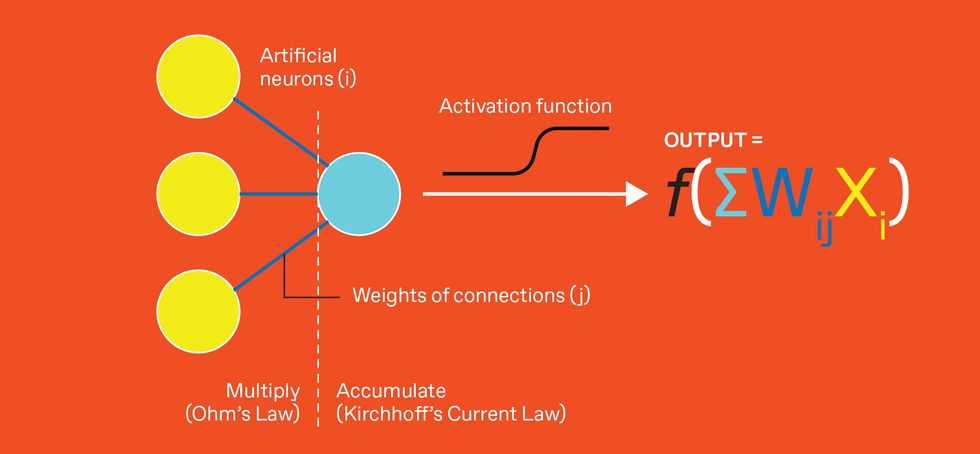
The most basic computation in an artificial neural network is called multiply and accumulate. The output of artificial neurons [left, yellow] are multiplied by the weight values connecting them to the next neuron [center, light blue]. That neuron sums its inputs and applies an output function. In analog AI, the multiply function is performed by Ohm's Law, where the neuron's output voltage is multiplied by the conductance representing the weight value. The summation at the neuron is done by Kirchhoff's Current Law, which simply adds all the currents entering a single node
The biggest time and energy costs in most computers occur when lots of data has to move between external memory and computational resources such as CPUs and GPUs. This is the "von Neumann bottleneck," named after the classic computer architecture that separates memory and logic. One way to greatly reduce the power needed for deep learning is to avoid moving the data—to do the computation out where the data is stored.
DNNs are composed of layers of artificial neurons. Each layer of neurons drives the output of those in the next layer according to a pair of values—the neuron's "activation" and the synaptic "weight" of the connection to the next neuron.
Most DNN computation is made up of what are called vector-matrix-multiply (VMM) operations—in which a vector (a one-dimensional array of numbers) is multiplied by a two-dimensional array. At the circuit level these are composed of many multiply-accumulate (MAC) operations. For each downstream neuron, all the upstream activations must be multiplied by the corresponding weights, and these contributions are then summed.
Most useful neural networks are too large to be stored within a processor's internal memory, so weights must be brought in from external memory as each layer of the network is computed, each time subjecting the calculations to the dreaded von Neumann bottleneck. This leads digital compute hardware to favor DNNs that move fewer weights in from memory and then aggressively reuse these weights.
A radical new approach to energy-efficient DNN hardware occurred to us at IBM Research back in 2014. Together with other investigators, we had been working on crossbar arrays of nonvolatile memory (NVM) devices. Crossbar arrays are constructs where devices, memory cells for example, are built in the vertical space between two perpendicular sets of horizontal conductors, the so-called bitlines and the wordlines. We realized that, with a few slight adaptations, our memory systems would be ideal for DNN computations, particularly those for which existing weight-reuse tricks work poorly. We refer to this opportunity as "analog AI," although other researchers doing similar work also use terms like "processing-in-memory" or "compute-in-memory."
There are several varieties of NVM, and each stores data differently. But data is retrieved from all of them by measuring the device's resistance (or, equivalently, its inverse—conductance). Magnetoresistive RAM (MRAM) uses electron spins, and flash memory uses trapped charge. Resistive RAM (RRAM) devices store data by creating and later disrupting conductive filamentary defects within a tiny metal-insulator-metal device. Phase-change memory (PCM) uses heat to induce rapid and reversible transitions between a high-conductivity crystalline phase and a low-conductivity amorphous phase.
Flash, RRAM, and PCM offer the low- and high-resistance states needed for conventional digital data storage, plus the intermediate resistances needed for analog AI. But only RRAM and PCM can be readily placed in a crossbar array built in the wiring above silicon transistors in high-performance logic, to minimize the distance between memory and logic.
We organize these NVM memory cells in a two-dimensional array, or "tile." Included on the tile are transistors or other devices that control the reading and writing of the NVM devices. For memory applications, a read voltage addressed to one row (the wordline) creates currents proportional to the NVM's resistance that can be detected on the columns (the bitlines) at the edge of the array, retrieving the stored data.
To make such a tile part of a DNN, each row is driven with a voltage for a duration that encodes the activation value of one upstream neuron. Each NVM device along the row encodes one synaptic weight with its conductance. The resulting read current is effectively performing, through Ohm's Law (in this case expressed as "current equals voltage times conductance"), the multiplication of excitation and weight. The individual currents on each bitline then add together according to Kirchhoff's Current Law. The charge generated by those currents is integrated over time on a capacitor, producing the result of the MAC operation.
These same analog in-memory summation techniques can also be performed using flash and even SRAM cells, which can be made to store multiple bits but not analog conductances. But we can't use Ohm's Law for the multiplication step. Instead, we use a technique that can accommodate the one- or two-bit dynamic range of these memory devices. However, this technique is highly sensitive to noise, so we at IBM have stuck to analog AI based on PCM and RRAM.
Unlike conductances, DNN weights and activations can be either positive or negative. To implement signed weights, we use a pair of current paths—one adding charge to the capacitor, the other subtracting. To implement signed excitations, we allow each row of devices to swap which of these paths it connects with, as needed.
Nonvolatile Memories for Analog AI
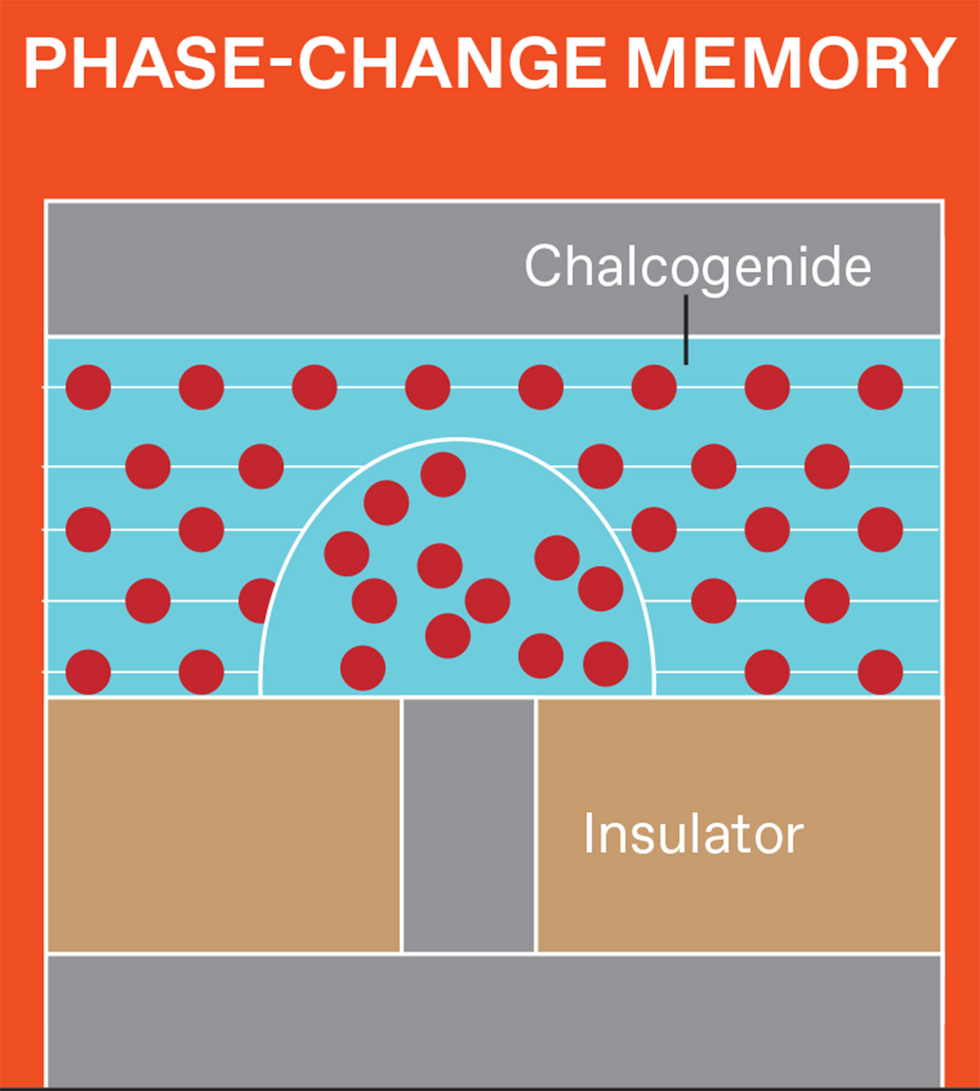
Phase-change memory's conductance is set by the transition between a crystalline and an amorphous state in a chalcogenide glass. In resistive RAM, conductance depends on the creation and destruction of conductive filaments in an insulator.
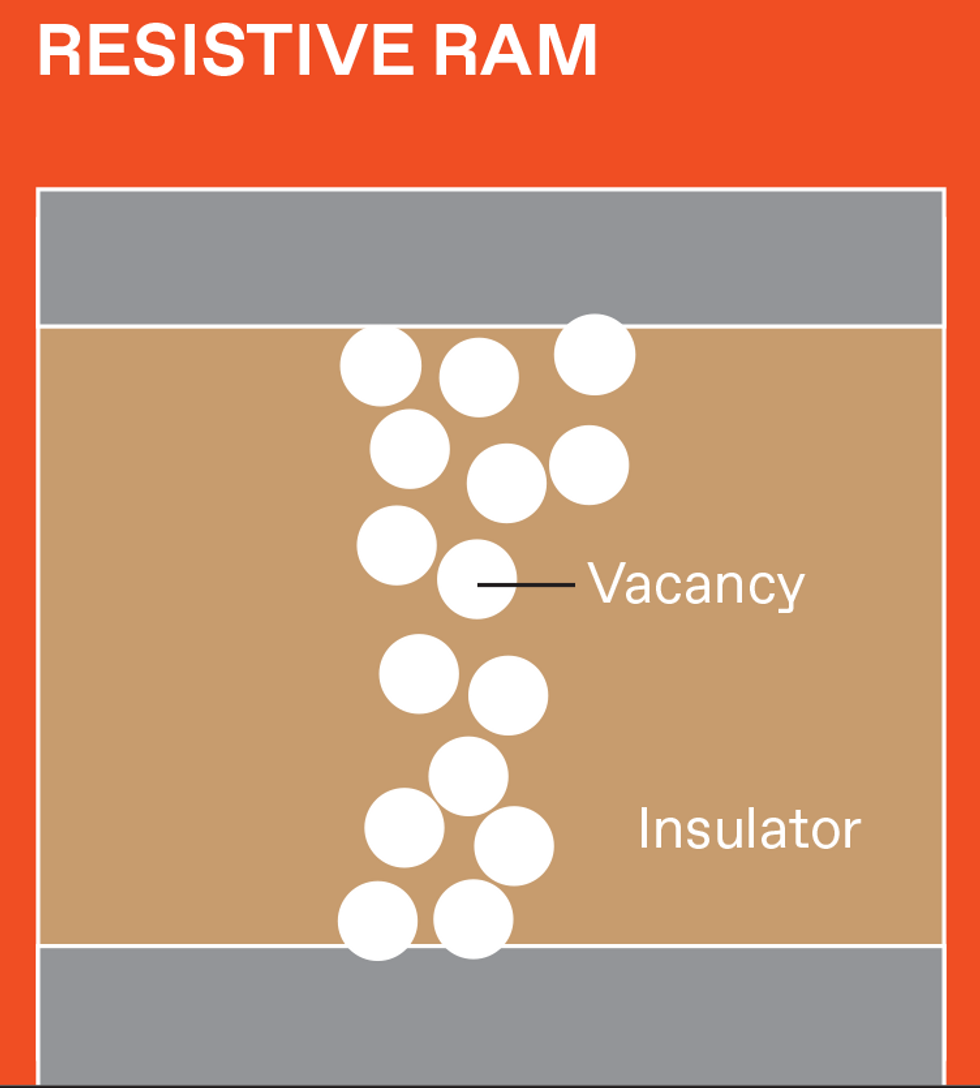
In resistive RAM, conductance depends on the creation and destruction of conductive filaments in an insulator.
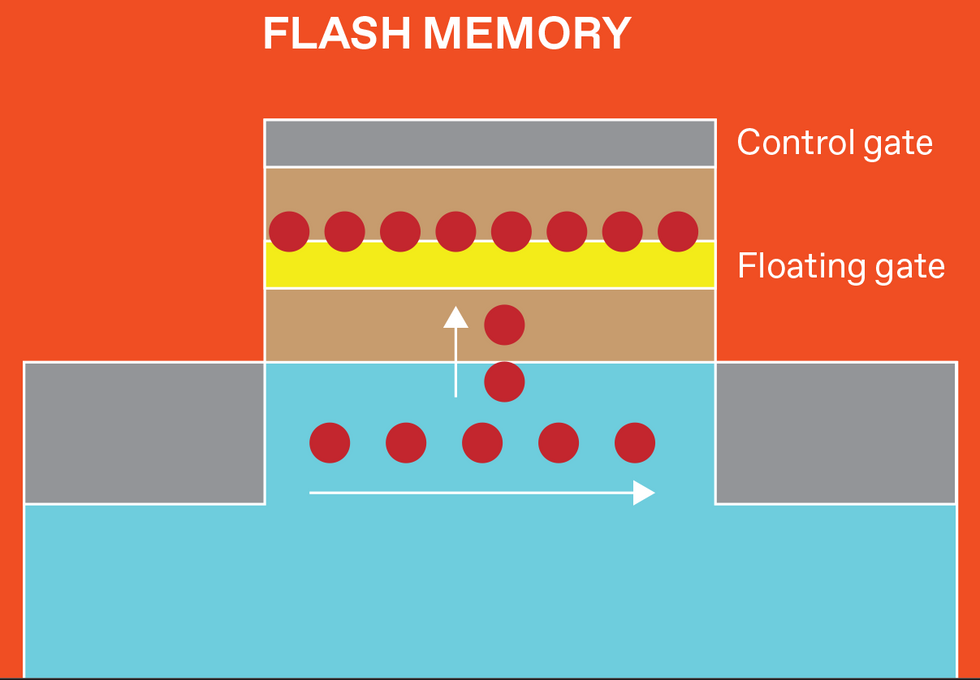
Flash memory stores data as charge trapped in a "floating gate." The presence or absence of that charge modifies conductances across the device.
Electrochemical RAM acts like a miniature battery. Pulses of voltage on a gate electrode modulate the conductance between the other two terminals by the exchange of ions through a solid electrolyte.
With each column performing one MAC operation, the tile does an entire vector-matrix multiplication in parallel. For a tile with 1,024 × 1,024 weights, this is 1 million MACs at once.
In systems we've designed, we expect that all these calculations can take as little as 32 nanoseconds. Because each MAC performs a computation equivalent to that of two digital operations (one multiply followed by one add), performing these 1 million analog MACs every 32 nanoseconds represents 65 trillion operations per second.
We've built tiles that manage this feat using just 36 femtojoules of energy per operation, the equivalent of 28 trillion operations per joule. Our latest tile designs reduce this figure to less than 10 fJ, making them 100 times as efficient as commercially available hardware and 10 times better than the system-level energy efficiency of the latest custom digital accelerators, even those that aggressively sacrifice precision for energy efficiency.
It's been important for us to make this per-tile energy efficiency high, because a full system consumes energy on other tasks as well, such as moving activation values and supporting digital circuitry.
There are significant challenges to overcome for this analog-AI approach to really take off. First, deep neural networks, by definition, have multiple layers. To cascade multiple layers, we must process the VMM tile's output through an artificial neuron's activation—a nonlinear function—and convey it to the next tile. The nonlinearity could potentially be performed with analog circuits and the results communicated in the duration form needed for the next layer, but most networks require other operations beyond a simple cascade of VMMs. That means we need efficient analog-to-digital conversion (ADC) and modest amounts of parallel digital compute between the tiles. Novel, high-efficiency ADCs can help keep these circuits from affecting the overall efficiency too much. Recently, we unveiled a high-performance PCM-based tile using a new kind of ADC that helped the tile achieve better than 10 trillion operations per watt.
A second challenge, which has to do with the behavior of NVM devices, is more troublesome. Digital DNNs have proven accurate even when their weights are described with fairly low-precision numbers. The 32-bit floating-point numbers that CPUs often calculate with are overkill for DNNs, which usually work just fine and with less energy when using 8-bit floating-point values or even 4-bit integers. This provides hope for analog computation, so long as we can maintain a similar precision.
Given the importance of conductance precision, writing conductance values to NVM devices to represent weights in an analog neural network needs to be done slowly and carefully. Compared with traditional memories, such as SRAM and DRAM, PCM and RRAM are already slower to program and wear out after fewer programming cycles. Fortunately, for inference, weights don't need to be frequently reprogrammed. So analog AI can use time-consuming write-verification techniques to boost the precision of programming RRAM and PCM devices without any concern about wearing the devices out.
That boost is much needed because nonvolatile memories have an inherent level of programming noise. RRAM's conductivity depends on the movement of just a few atoms to form filaments. PCM's conductivity depends on the random formation of grains in the polycrystalline material. In both, this randomness poses challenges for writing, verifying, and reading values. Further, in most NVMs, conductances change with temperature and with time, as the amorphous phase structure in a PCM device drifts, or the filament in an RRAM relaxes, or the trapped charge in a flash memory cell leaks away.
There are some ways to finesse this problem. Significant improvements in weight programming can be obtained by using two conductance pairs. Here, one pair holds most of the signal, while the other pair is used to correct for programming errors on the main pair. Noise is reduced because it gets averaged out across more devices.
We tested this approach recently in a multitile PCM-based chip, using both one and two conductance pairs per weight. With it, we demonstrated excellent accuracy on several DNNs, even on a recurrent neural network, a type that's typically sensitive to weight programming errors.
Vector-Matrix Multiplication with Analog AI
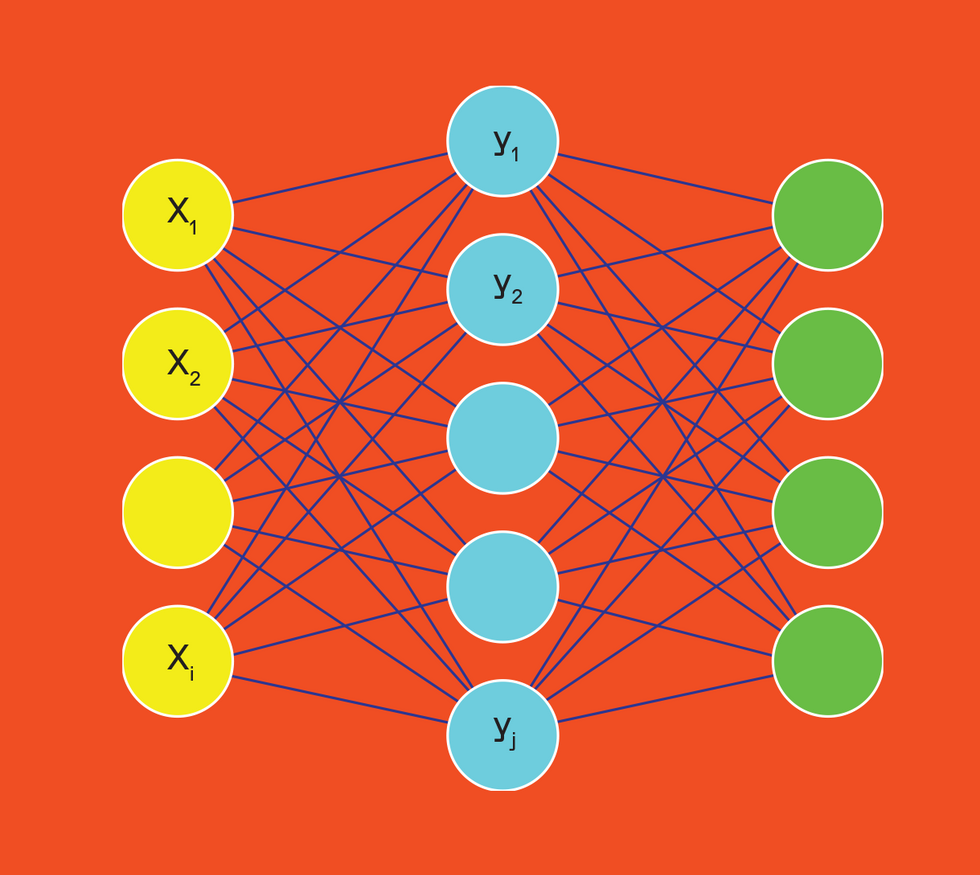
Vector-matrix multiplication (VMM) is the core of a neural network's computing [top]; it is a collection of multiply-and-accumulate processes. Here the activations of artificial neurons [yellow] are multiplied by the weights of their connections [light blue] to the next layer of neurons [green].
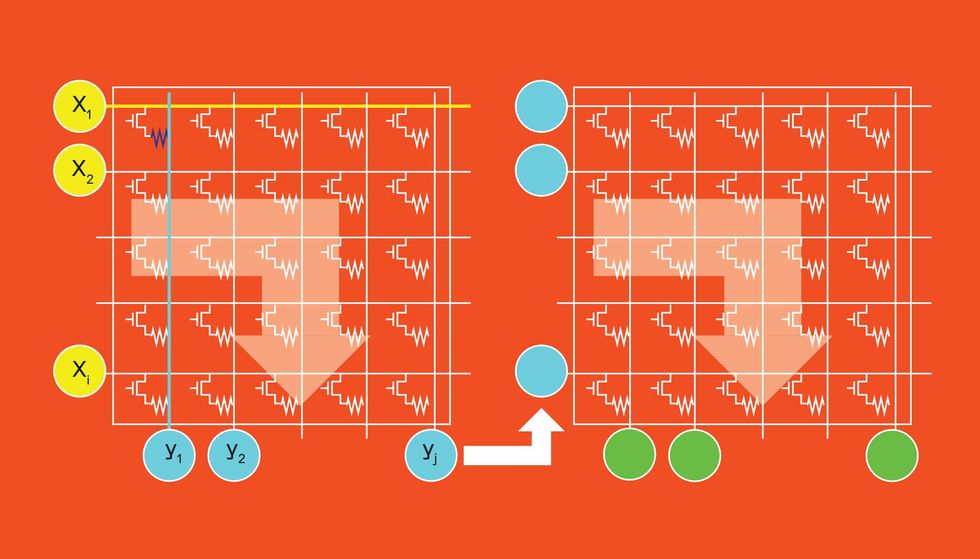
For analog AI, VMM is performed on a crossbar array tile [center]. At each cross point, a nonvolatile memory cell encodes the weight as conductance. The neurons' activations are encoded as the duration of a voltage pulse. Ohm's Law dictates that the current along each crossbar column is equal to this voltage times the conductance. Capacitors [not shown] at the bottom of the tile sum up these currents. A neural network's multiple layers are represented by converting the output of one tile into the voltage duration pulses needed as the input to the next tile [right].
Different techniques can help ameliorate noise in reading and drift effects. But because drift is predictable, perhaps the simplest is to amplify the signal during a read with a time-dependent gain that can offset much of the error. Another approach is to use the same techniques that have been developed to train DNNs for low-precision digital inference. These adjust the neural-network model to match the noise limitations of the underlying hardware.
As we mentioned, networks are becoming larger. In a digital system, if the network doesn't fit on your accelerator, you bring in the weights for each layer of the DNN from external memory chips. But NVM's writing limitations make that a poor decision. Instead, multiple analog AI chips should be ganged together, with each passing the intermediate results of a partial network from one chip to the next. This scheme incurs some additional communication latency and energy, but it's far less of a penalty than moving the weights themselves.
Until now, we've only been talking about inference—where an already-trained neural network acts on novel data. But there are also opportunities for analog AI to help train DNNs.
DNNs are trained using the backpropagation algorithm. This combines the usual forward inference operation with two other important steps—error backpropagation and weight update. Error backpropagation is like running inference in reverse, moving from the last layer of the network back to the first layer; weight update then combines information from the original forward inference run with these backpropagated errors to adjust the network weights in a way that makes the model more accurate.
The Tiki-Taka Solution
Analog AI can reduce the power consumption of training neural networks, but because of some inherent characteristics of the nonvolatile memories involved, there are some complications. Nonvolatile memories, such as phase-change memory and resistive RAM, are inherently noisy. What's more, their behavior is asymmetric. That is, at most points on their conductance curve, the same value of voltage will produce a different change in conductance depending on the voltage's polarity.
One solution we came up with, the Tiki-Taka algorithm, is a modification to backpropagation training. Crucially, it is significantly more robust to noise and asymmetric behavior in the NVM conductance. This algorithm depends on RRAM devices constructed to conduct in both directions. Each of these is initialized to their symmetry point—the spot on their conductance curve where the conductance increase and decrease for a given voltage are exactly balanced. In Tiki-Taka, the symmetry-point-balanced NVM devices are involved in weight updates to train the network. Periodically, their conductance values are programmed onto a second set of devices, and the training devices are returned to their natural symmetry point. This allows the neural network to train to high accuracy, even in the presence of noise and asymmetry that would completely disrupt the conventional backpropagation algorithm.
The backpropagation step can be done in place on the tiles but in the opposite manner of inferencing—applying voltages to the columns and integrating current along rows. Weight update is then performed by driving the rows with the original activation data from the forward inference, while driving the columns with the error signals produced during backpropagation.
Training involves numerous small weight increases and decreases that must cancel out properly. That's difficult for two reasons. First, recall that NVM devices wear out with too much programming. Second, the same voltage pulse applied with opposite polarity to an NVM may not change the cell's conductance by the same amount; its response is asymmetric. But symmetric behavior is critical for backpropagation to produce accurate networks. This is only made more challenging because the magnitude of the conductance changes needed for training approaches the level of inherent randomness of the materials in the NVMs.
There are several approaches that can help here. For example, there are various ways to aggregate weight updates across multiple training examples, and then transfer these updates onto NVM devices periodically during training. A novel algorithm we developed at IBM, called Tiki-Taka, uses such techniques to train DNNs successfully even with highly asymmetric RRAM devices. Finally, we are developing a device called electrochemical random-access memory (ECRAM) that can offer not just symmetric but highly linear and gradual conductance updates.
The success of analog AI will depend on achieving high density, high throughput, low latency, and high energy efficiency—simultaneously. Density depends on how tightly the NVMs can be integrated into the wiring above a chip's transistors. Energy efficiency at the level of the tiles will be limited by the circuitry used for analog-to-digital conversion.
But even as these factors improve and as more and more tiles are linked together, Amdahl's Law—an argument about the limits of parallel computing—will pose new challenges to optimizing system energy efficiency. Previously unimportant aspects such as data communication and the residual digital computing needed between tiles will incur more and more of the energy budget, leading to a gap between the peak energy efficiency of the tile itself and the sustained energy efficiency of the overall analog-AI system. Of course, that's a problem that eventually arises for every AI accelerator, analog or digital.
The path forward is necessarily different from digital AI accelerators. Digital approaches can bring precision down until accuracy falters. But analog AI must first increase the signal-to-noise ratio (SNR) of the internal analog modules until it is high enough to demonstrate accuracy equivalent to that of digital systems. Any subsequent SNR improvements can then be applied toward increasing density and energy efficiency.
These are exciting problems to solve, and it will take the coordinated efforts of materials scientists, device experts, circuit designers, system architects, and DNN experts working together to solve them. There is a strong and continued need for higher energy-efficiency AI acceleration, and a shortage of other attractive alternatives for delivering on this need. Given the wide variety of potential memory devices and implementation paths, it is quite likely that some degree of analog computation will find its way into future AI accelerators.
This article appears in the December 2021 print issue as "Ohm's Law + Kirchhoff's Current Law = Better AI."
- Startup and Academics Find Path to Powerful Analog AI - IEEE ... ›
- To Speed Up AI, Mix Memory and Processing - IEEE Spectrum ›
- IBM Toolkit Aims at Boosting Efficiencies in AI Chips - IEEE Spectrum ›
- When AI “Played” Math, It Cracked an Internet Chokepoint - IEEE Spectrum ›
- Computing with Chemicals Makes Faster, Leaner AI - IEEE Spectrum ›
- None ›


