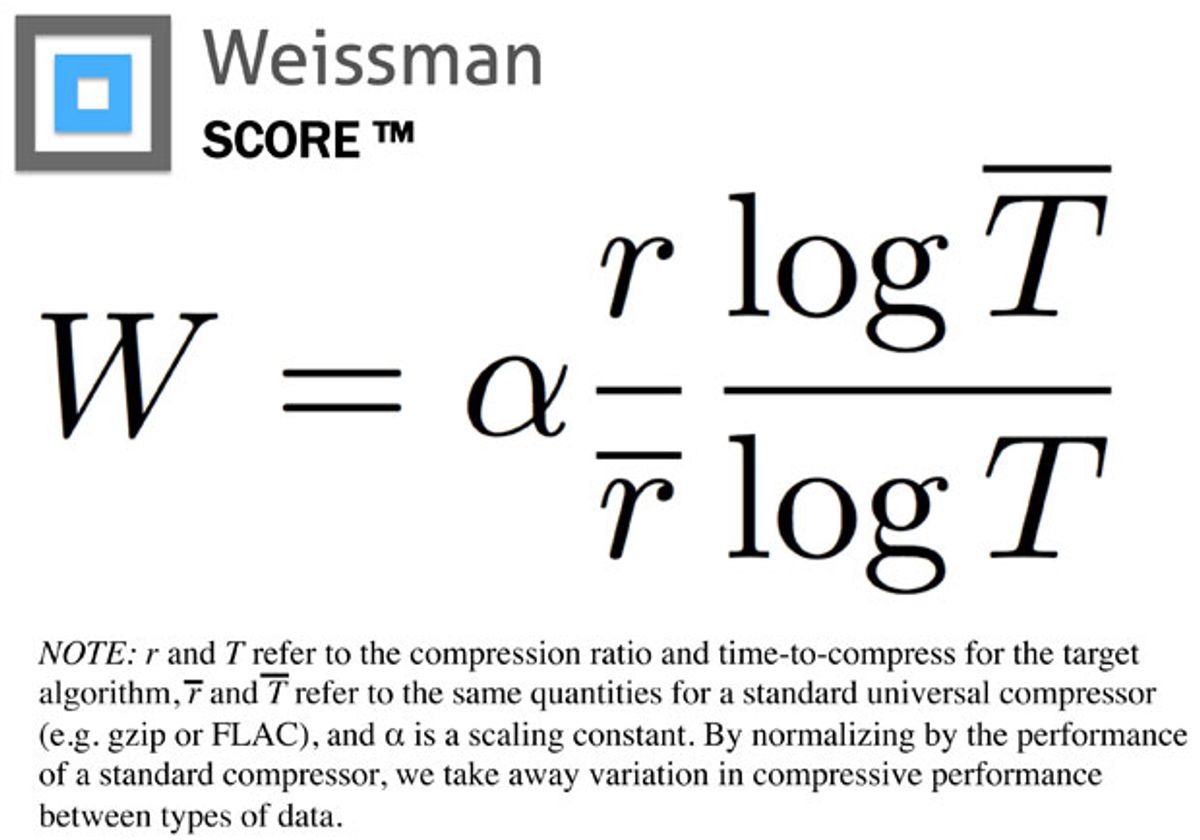When the creators of the HBO TV series Silicon Valley decided that the show would hinge around a breakthrough compression algorithm, they had a problem.
It’s hard to convey to a lay audience that one compression algorithm is better than another—you could compress and decompress images, say, with some loss and look for glitches in the resulting image, but they are hard to spot. But metrics for compression algorithms that rate not only the amount of compression but the processing speed, are hard to find. So it asked the consultants it brought in to help develop the original algorithm—Stanford Professor Tsachy Weissman and then-PhD student Vinith Misra—to come up with a metric that could be used to score multiple algorithms and find a winner. (Misra recently graduated and will soon be working on IBM’s Watson project.)
It seems that someone would have come up with such a metric by now. But, says Weissman, “there are two communities: the practitioners, who care about running time, and the theoreticians, who care about how succinctly you can represent the data and don’t worry about the complexity of the implementation.” As a result of this split, he says, no one had yet combined, in a single number, a means of rating both how fast and how tightly an algorithm compresses.
Misra came up with a formula (photo above), incorporating both. Along with existing benchmarks the formula creates a metric that the show writers tagged the “Weissman Score.” It's not a fictional metric: although it didn’t exist before Misra created it for the show, it works and may soon find use in the real world.
“It is essentially the compression ratio and the ratio of the log of the compression time,” Misra explains, “but it then normalizes that number against an industry standard compressor used for the same data. For music, say, we’d use might use FLAC.” (FLAC, or Free Lossless Audio Codec is an open format from the Xiph.org foundation.)
“I don’t want to be one who promotes a metric carrying my name,” Weissman says, “but I am tempted to use it. I’m writing a paper with a student of mine on genomic data compression in which we talk about improving a previously-used scheme. We’ve created a table with two columns showing compression rate and compression time of different algorithms,” he says, but it would have been more effective to show, in addition, a comparative measure that factors both, like the Weissman score. He won’t succumb to temptation this time.
But other researchers, who don’t have to worry about the perception of being self-promoters, are poised to use the metric. Dror Baron, an assistant professor of electrical and computer engineering at North Carolina State University, believes the Weissman Score is a valuable metric. He recently presented a paper at the recent IEEE International Symposium on Information Theory and, in future versions of that paper, plans to replace the scatter graph he used to show the efficacy of compression algorithms with a set of Weissman scores.
Marcelo Weinberger, a distinguished scientist at the center for the Science of Information, currently in residence at Stanford, is also considering incorporating the metric into a course in order "to put some 'Valley-life' into an otherwise mathematical and abstract subject," he says. The Weissman Score could also lead students to think about the fundamental limits of compression and complexity trade-offs.
And Jerry Gibson, a professor at the University of California at Santa Barbara, says he's going to introduce the metric into two classes this year. For a winter quarter class on information theory, he will ask students to use the score to evaluate lossless compression algorithms. In a spring quarter class on multimedia compression, he will use the score in a similar way, but in this case, because the Weissman Score doesn't consider distortion introduced in lossy compression, he will expect the students to weight that factor as well. In both cases Gibson plans to introduce the metric without mentioning its link to a TV series. "I will leave that for them to discover," he says.
For more on the compression algorithms in HBO's Silicon Valley, see "A Made-For-TV Compression Algorithm."
Tekla S. Perry is a senior editor at IEEE Spectrum. Based in Palo Alto, Calif., she's been covering the people, companies, and technology that make Silicon Valley a special place for more than 40 years. An IEEE member, she holds a bachelor's degree in journalism from Michigan State University.