The male albatross is finally back from his foraging, and now there is no time to lose. His mate has been patiently sitting on their nest awaiting his return, without food, for nearly a month, and we have to get to her before she flies off to forage for herself.
Our colleague, biologist Anna Nesterova, crawls slowly toward the bird. All of a sudden, she lunges: With her left hand she expertly grabs the 10-kilogram albatross by the beak, and with her right arm she hugs its body and lifts it off the nest and its precious cargo, a single egg. Together we then fix a GPS logger onto the feathers of the bird’s back with adhesive tape and glue.
Soon after we release her, the mother albatross takes two or three steps into the furious wind, opens her 3-meter-wide wings, and takes flight. Four weeks from now, she’ll return to this island in the southern Indian Ocean bearing a data log of where and how she flew—data that at last will put to the test our theories of how she stays aloft so long, almost never touching down, barely even flapping her long, elegant wings. If we could get our aerial robots to emulate that feat, they might someday orbit Earth for months, surfers of the winds of the uttermost sky.
Since at least the 1880s, scientists have wondered how the wandering albatross (Diomedea exulans), soars for as long and as far as it does, over open water, without a bit of thermal updraft. It’s no accident that the bird makes its home in exceptionally windy places—the wind is essential for such a heavy animal to get airborne in the first place. Once in the air, the bird performs a flying trick that seems to involve characteristic repetitive up and down maneuvers, sometimes dipping nearly to the water’s surface, and all in the face of more wind than most cruise passengers can withstand without going green with seasickness.
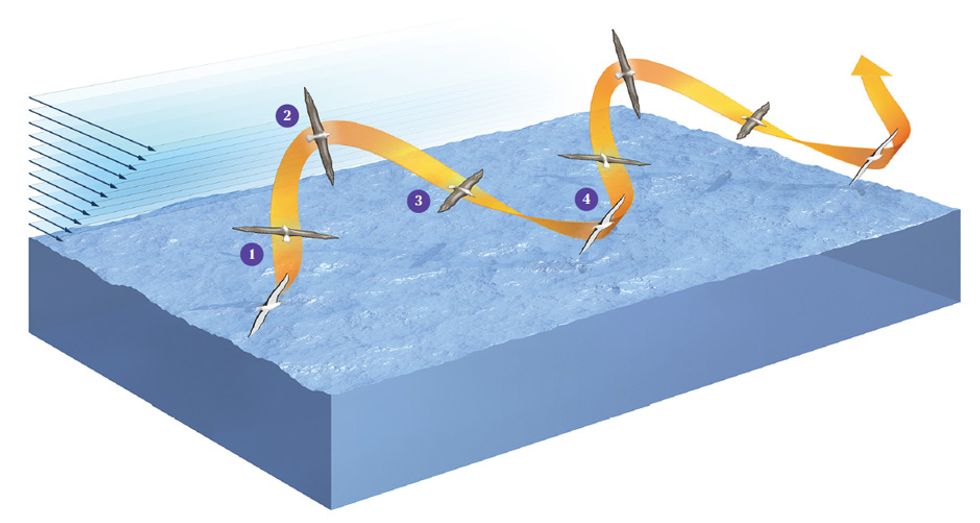
This type of flight is known as dynamic soaring. Just watch an albatross, and you can easily discriminate its four phases of flight: There’s a windward climb, then a curve from windward to leeward at peak altitude, then a leeward descent, and finally a reverse turn close to the sea surface that leads seamlessly into the next cycle of flight.
Although any human pilot who tried to use dynamic soaring to take passengers from Munich to New York City would lose his license 2 minutes after landing, a computer that’s controlling an unmanned aerial vehicle, or UAV, isn’t quite so constrained. The engineers who program it need merely to understand this trick of nature and adapt it to their ends. And this is exactly what we are up to.
Students of the albatross’s flight understood early on that the bottommost layer of wind blowing above any surface, including that of water, will incur friction and thus slow down. This layer itself then becomes an obstacle that slows the layer just above it (though not by much), in a process that continues upward. The result is a 10- to 20-meter-high region known as a boundary layer or shear wind field, through which the wind speed increases smoothly and dramatically the higher you go in the field. Dynamic soaring maneuvers extract energy from that field, enabling the albatross to fly in any direction, even against the wind, with hardly any effort.
Exactly how the bird extracts energy from a horizontally blowing wind, however, was a puzzle. Scientists over the decades have attempted to find the solution using increasingly sophisticated computer simulations. Yet elaborate as they may be, these models can’t capture the full complexity of what’s happening. How do you simulate, for example, a sea troubled by strong winds that breaks up into irregular, meter-high waves, chopping the air into discontinuous blocks? Because of such unknowns, researchers long debated whether the shear wind field alone explained the soaring or whether there might also be other effects, such as gusts or vertical wind components.
We finally resolved this controversy at the Institute of Flight System Dynamics, at the Technische Universität München (Munich University of Technology), using an optimization method known as periodic optimal control. This same methodology had previously proved effective in aeronautical engineering, to calculate the aircraft trajectory that saves the most fuel, for example.
At the institute, we had also used it to optimize the flight trajectories of space gliders to deal with emergency cases. Under normal conditions, the vehicle would just glide home, adjusting its attitude with tiny thrusters and flaps and other aerodynamic control surfaces. But it also had to be able to survive failures of the control surfaces. So we looked at the interaction between the vehicle’s glide and Earth’s gravitational field and atmosphere, with an eye toward minimizing the thrusters’ consumption of propellant. We also had to factor in the time of failure, possible airfields for landing, and the physical limitations of the vehicle, such as maximum g-load factor and maximum heat flow.
When we set out to apply optimization theory to the albatross, some groundwork had already been laid. The drag and lift characteristics of the bird, for example, had been analyzed back in the 1920s by Pierre Idrac of France; in the 1960s by Vance A. Tucker and G. Christian Parrott [PDF] of the United States and by M. Berger & Wolfgang Göhde of Germany; and in the 1980s by Colin J. Pennycuick [PDF] of the United Kingdom. Furthermore, the distribution of the wind speed above the sea surface had been well described in previous research.
Combining these results, we worked out a set of differential equations that describe the dynamics of flight. We also expressed the wind profile close to the water’s surface as a function of the wind speed at higher altitudes. Together, the two elements of our model were able to simulate the flight of the bird based on the lift coefficient, the bank angle, and the wind speed.
We then plugged our model into high-performance optimal control tools. We instructed our computer program to find the control inputs that would yield a trajectory an albatross could trace without flapping its wings under the following constraints: first, that the direction of flight and the total energy state—the sum of kinetic and potential energies—were the same at the beginning and the end of a flight cycle (as it must be in the endlessly repeating soaring cycle); and second, that the program search for the maneuver that worked at the lowest possible wind speed.
The result we got was a minimum wind speed of 8.6 to 8.9 meters per second, at a reference altitude of 10 meters. Our boundary condition ensured that the predicted trajectory would be energy neutral, so that once started it would continue to repeat itself.
Our model thus predicted that albatrosses could soar dynamically as long as the wind speed is a bit more than 30 kilometers per hour (16 knots). It is no coincidence, then, that these birds live in the far southern latitudes known as the Roaring Forties and the Furious Fifties, where typical wind speeds are much higher than that. What is more, our results indicated that the shear wind field alone could enable the flight of the birds. No effects from waves, turbulence, or anything else are required. Proving our calculations, however, required getting some real measurements.
The Kerguelen Islands are a base for wandering albatrosses, which circumnavigate the Furious Fifties and other latitudes of the uttermost south.
To prove the theory experimentally, we knew we would need to capture the albatross’s quick-changing flight vectors. The meter-level accuracy and once-per-second readings of the GPS receiver in your car aren’t fine grained enough for that job. We needed decimeter precision and an update rate of 10 hertz. We did find some geodetic units that deliver GPS readings to the centimeter level, but they came with constraints that no wandering albatross would stomach: hardware far too big and heavy to fly with, a range to the base station’s receiver far shorter than the bird naturally travels, and, in many cases, an initial calibration that would require the bird to stay completely still for up to 15 minutes.
After some head scratching, we came up with a solution: We used miniaturized mass-market receivers that normally calculate positions to meter-level accuracy at 1 Hz. But instead of having the device calculate its position in real time, we rigged it to log GPS raw data at 10 Hz, so that we could process the information at our leisure, back in the office. We were able to do this because we didn’t care about the unit’s absolute accuracy, only its precision—that is, we wanted to know the shape of a particular soaring maneuver relative to its starting point, wherever that starting point might be. And so we didn’t need to initialize the system or keep it close to a base station.
We came up with a novel, time-differential algorithm that exploits the same type of raw measurements used by most geodesy software: highly precise albeit ambiguous measurements of the phase of a GPS satellite’s carrier signal (or L1). Normally, a navigation system will rely mainly on tracking a coarse yet robust code modulated on a high-frequency carrier signal. That way the system can measure the absolute distance between the receiver and each satellite in view to within a meter. Our strategy of directly exploiting the fragile carrier signal let us measure merely the change in the range since signal acquisition, but to do so to within a centimeter. We could thus precisely distill dynamic soaring maneuvers out of the carrier-phase data without knowing exactly where the maneuvers started.
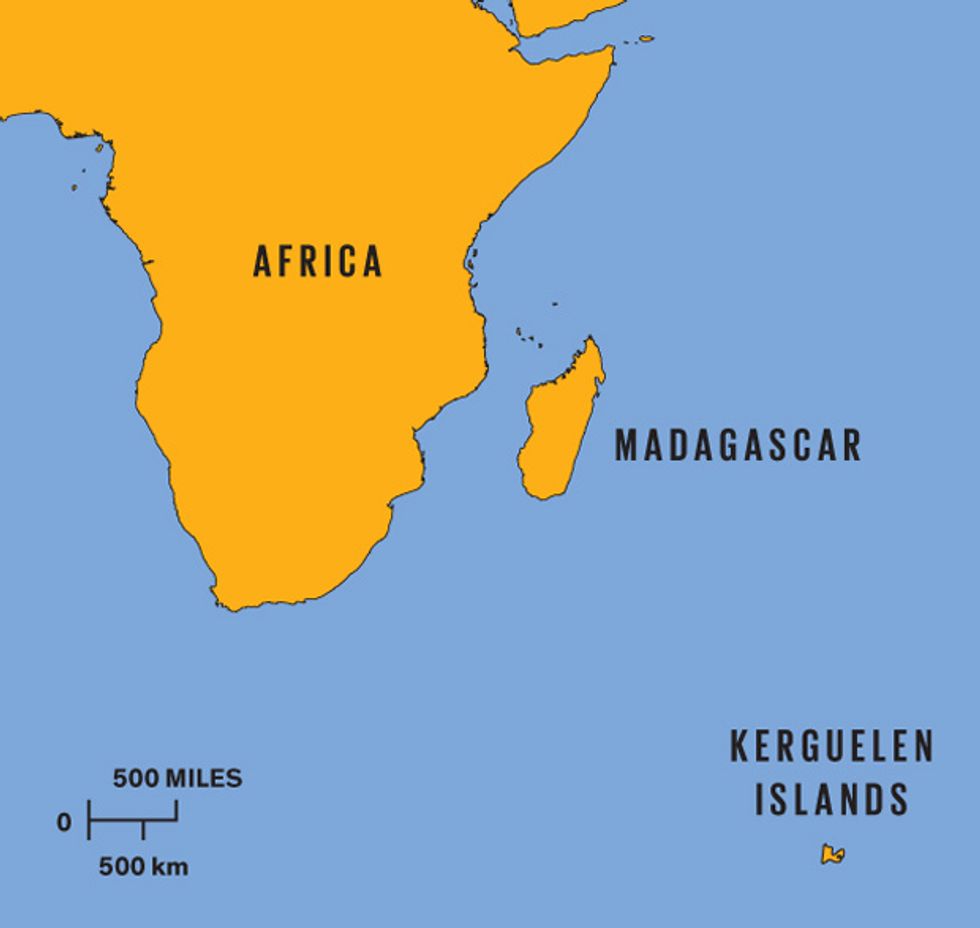
In December 2008, two of us (Traugott and Nesterova) headed out to the field to put our ideas and our equipment to the test. We flew to Réunion, east of Madagascar; the French island constitutes one of the outermost parts of the eurozone. There we boarded the southbound French research vessel Marion Dufresne II. Two weeks later we reached the Kerguelen Islands, 2800 kilometers east of South Africa, getting off at the research station in Port-aux-Français. We then had an 8-hour eastward hike to our base camp, a simple hut without running water or electricity. Our expedition included several other researchers working with two French organizations: the Center for Functional and Evolutionary Ecology, directed by Francesco Bonadonna of the University of Montpellier, and the French Polar Institute Paul Émile Victor.
Nesterova, the biologist, had come mainly to study king penguins, not albatrosses. But it was well that she was there. As an aerospace engineer, Traugott had never handled a wild animal, much less one with a beak as long and sharp as a carving knife; he had never even seen a wandering albatross up close.
One of our main tasks during the six weeks we spent in the field was to watch for the brief changings of the guard between breeding pairs. Only at such a hand-off could we capture and tag a bird we knew would fly out soon. We kept an eye on about 35 albatross nests scattered quite widely in the vicinity of our hut. We had permission from the French administration of the archipelago to fit up to 20 birds with loggers, and we didn’t want to miss a single opportunity.
We equipped our first bird the week before Christmas. The procedure by which we mounted the GPS logger has been widely used by other researchers; it exposes the animals to a minimum stress level, and, just as important, it keeps the device in place. We taped the logger to second-layer feathers right below the shoulder joints and secured the tape with superglue.
Three days later, our first bird returned. As Traugott approached the nest, his heart was pounding. But the GPS logger was gone! All that effort for a small piece of electronics that now lay at the bottom of the ocean. Head bowed, he returned to the hut to tell Nesterova. She frowned. “Let’s have a closer look,” she said. Back at the nest, our bird had already taken over for his mate, who had left to go find breakfast.
Nesterova crawled to the nest, took the bird firmly but gently in hand, and then carefully examined it. The logger was still there! It had simply been covered up with plumage. We used a pair of scissors to cut the tape. Finally we had the bird’s precious payload in our hands.
Approaching a Man-size nesting bird requires tact, but no harm is done in gluing an ultralight GPS logger onto the back feathers. There it can track the bird’s flight over many days.Photo: Johannes Traugott
Back in the hut, we eagerly downloaded the data to a laptop. The in-depth processing would be done back in our Munich office, but we wanted to find out if we had managed to log any in-flight data, how good the data were, and whether we needed to tweak some system parameters to make the next logging trip more successful. Indeed, a first check revealed that the raw data on the carrier phase were not of the quality we’d hoped for, but still good enough to work with. It seems that the quality problem stemmed partly from the multiple paths taken by the reflections of the signal from the waves. Processing this data back in Munich was challenging.
Back home, our analysis continued. As we described earlier, dynamic soaring involves a climb into the wind, a curve to leeward, a leeward descent, and a reverse turn close to the sea surface, where the cycle begins anew. Our measurements were the first to demonstrate that the total energy in these maneuvers is the same at the beginning and the end of the trajectory. We also found that the closer the bird got to the water’s surface, the lower the total energy; right near the water, there was no gain at all. Our work therefore proved that the waves and related turbulence play no significant role in the bird’s flight. We discovered that total energy tops out after the bird makes its upper turn, so this has to be the part of the cycle in which it extracts the most energy from the wind.
On top of this energy analysis we looked at the aerodynamic forces acting on the bird, which were quite complex. The essence is as follows: The local shear wind lets the bird change the direction of the lift it generates as a kind of propulsive force during the upper curve of the cycle. At that moment, the strong wind acts like a kind of outboard engine. Afterward, the bird dives close to the water and then turns back up, in the process incurring a braking effect. The bird still has a “propulsion profit” over the whole cycle that just manages to overcome drag. As long as it keeps up that pattern of dips, swoops, and turns, it can keep on flying—flying for free.
In short, the insights offered by our GPS measurements largely confirmed the findings of our optimization-based analysis. We now know a lot more about the fascinating flight of these beautiful animals than we did before. Of course, there is always room for refinement.
For one thing, we weren’t able to measure the birds’ air speed directly because any appropriate sensor, such as a pitot tube, would stick out of the plumage quite a bit—probably enough to affect flight and surely enough to annoy the birds. Instead we had to rely on rather coarse remote wind information provided by satellite measurements (QuickSCAT ocean surface wind vectors).
In the future, we’d also like to measure attitude—the angles of roll, pitch, and yaw. The rapid development of inertial sensors made with microelectromechanical systems should allow us to do that the next time around.
This project is more than a sideline in natural history. The open sea isn’t the only place that offers a shear wind field suitable for dynamic soaring, and wandering albatrosses aren’t the only pilots that rely on it to conserve energy. Such boundary layers also exist within the high-altitude jet streams that encircle Earth; even though these layers are much thicker than the one the albatross flies in, the physics are the same. That means that UAVs with the proper aerodynamics and programming might one day exploit them to stay aloft for weeks or months on end, allowing them to serve as surveillance nodes or radio relay links.
And indeed, flight optimizations we’ve done in related research show that aircraft having the aerodynamics of today’s gliders or sailplanes could perform sustained dynamic soaring in these atmospheric layers by accordingly scaled maneuvers. “Surfing the jet stream” is no mere fantasy; it is a reasonable strategy for aeronautical engineers to pursue.
This article originally appeared in print as “The Flight of the Albatross.”
About the Authors
When Gottfried Sachs, a professor of flight mechanics and flight control at Technische Universität München, suggested that Johannes Traugott do his doctoral thesis on albatross flight, Traugott says he jumped at “the once-in-a-lifetime chance” to combine his interests in algorithms, flying, and sailing. Traugott now develops navigation tools for Trimble Navigation, of Sunnyvale, Calif. Anna Nesterova, a biologist at the Center for Functional Ecology and Evolution, in Montpellier, France, collaborated on the albatross study while researching the navigation of penguins; she is now a postdoc at the University of Oxford.